Mit einem Oszilloskop wird die Zeitabhängigkeit von zwei Sinussignalen, wie in Abbildung 10.1 dargestellt, gemessen.
import numpy as np
import matplotlib.pylab as plt
# Oszi-Plot
t = np.linspace(-10e-3, 10e-3, 100)
T = 8e-3
f = 1 / T
w = 2 * np.pi * f
A1 = 15
A2 = 10
dt = 1e-3
# Spannungen
u1 = -A1 * np.cos(w * t)
u2 = A2 * np.cos(w * (t - dt))
# Setting figure properties
plt.figure(1)
plt.plot(t, u1, label=r"$u_1(t)$")
plt.plot(t, u2, label=r"$u_2(t)$")
plt.axis([-5e-3, 5e-3, -20, 20])
plt.grid()
plt.xlabel('Zeit t/s')
plt.ylabel('Spannung u/V')
plt.legend()
plt.show()
Geben Sie für die Spannungen \(u_1(t)\) und \(u_2(t)\) folgende Größen an:
die Periodendauer \(T\)
die Frequenz \(f\)
die Kreisfrequenz \(\omega\).
\[ T = 8\,ms \]
\[ f = \frac{1}{T}=125\,Hz \]
\[ \omega = 2\pi f = 785\,1/s \]
Geben Sie für die Darstellungen der Sinus- und Kosinussignale \(u_i(t) = \hat{U}_i \sin(\omega t + \varphi_{ui})\) und \(u_i(t) = \hat{U}_i \cos(\omega t + \psi_{ui})\) die Amplituden \(\hat{U}_i\) und die Phasen \(\varphi_{ui}\) und \(\psi_{ui}\) mit \(i=1,2\) an.
Die Amplituden der Spannungen sind \(\hat{U}_1=15\,V\) und \(\hat{U}_2=10\,V\). Die zeitlichen Verläufen können dann wie folgt angegeben werden:
\[ u_1(t) = -\hat{U}_1 \cos(\omega t) = \hat{U}_1 \cos(\omega t \pm \pi) \]
\[ u_1(t) = \hat{U}_1 \sin\left(\omega t - \frac{\pi}{2}\right) \]
\[ u_2(t) = \hat{U}_2 \cos(\omega(t- 1\,ms)) = \hat{U}_2 \cos\left(\omega t - \frac{\pi}{4}\right); \]
\[ u_2(t) = \hat{U}_2 \sin\left(\omega t + \frac{\pi}{4}\right) \]
Wenn \(u_1(t)\) die Eingangsspannung und \(u_2(t)\) die Ausgangsspannung einer Schaltung bedeuten, wie groß ist dann der komplexe Übertragungsfaktor \(\underline{H} = \underline{U}_2 / \underline{U}_1\) der Schaltung?
Die Umrechnung der reellen Spannungsverläufe in komplexe Größen geschieht über die Funktionaltransformation.
\[\begin{align} u(t) &= \operatorname{Re}\left\{\underline{u}(t)\right\} \\ &= \operatorname{Re}\left\{\underline{\hat{U}}e^{j\omega t}\right\} \\ &= \operatorname{Re}\left\{\hat{U}e^{j(\omega t+\varphi_u)}\right\} \\ &= \operatorname{Re}\left\{\hat{U}e^{j\omega t}e^{j\varphi_u}\right\} \\ &= \operatorname{Re}\left\{\hat{U}\cos(\omega t + \varphi_u) + j \hat{U} \sin(\omega t + \varphi_u) \right\} \end{align}\]
\[ \underline{u}(t) = \underline{\hat{U}}e^{j\omega t} \quad \mbox{rotierender Zeiger, komplexer Momentanwert} \]
\[ \underline{u}(0) = \underline{\hat{U}}e^{j0}=\hat{U}e^{j\varphi_u} \quad \mbox{ruhender Zeiger, komplexer Scheitelwert} \]
\[ \underline{U} = \frac{1}{\sqrt{2}}\hat{U} e^{j\varphi_u} \quad \mbox{komplexer Effektivwert} \]
\[ \underline{U}_1 = \frac{1}{\sqrt{2}} \hat{U}_1 e^{- j \pi} \]
\[ \underline{U}_2 = \frac{1}{\sqrt{2}} \hat{U}_2 e^{-j\frac{\pi}{4}} \]
\[\begin{align} \underline{H} &= \frac{\underline{U}_2}{\underline{U}_1} \\ &= \frac{\hat{U}_2 e^{-j\frac{\pi}{4}}}{\hat{U}_1 e^{- j \pi}} \\ &= \frac{\hat{U}_2}{\hat{U}_1} e^{j (-\frac{\pi}{4}+\pi)} \\ &= \frac{2}{3} e^{j \frac{3}{4}\pi} \end{align}\]
Zeichnen Sie in das Oszillogramm den Verlauf der Spannung \(u_3(t)\) mit der Frequenz \(f=100\,Hz\) und dem komplexen Scheitelwert \(\underline{\hat{U}}_3 = (15-j 20)\,V\) (karthesische Koordinaten) ein.
Darstellung des komplexen Scheitelwertes \(\underline{\hat{U}}_3\) in Polarkoordinaten, Betrag und Phase.
\[ \underline{\hat{U}}_3 = \sqrt{15^2 + 20^2} \exp \left(j \,\arctan\left(\frac{-20}{15}\right)\right) = 25 e^{-j 0.927} \]
\[ u_3(t) = \operatorname{Re}\left\{\underline{\hat{U}}_3e^{j\omega_3 t}\right\} = 25\,V \cos(\omega_3 t - 0.927) = 25\,V \cos\left(\omega_3 (t - 1.43\,ms)\right) \]
import numpy as np
import matplotlib.pylab as plt
# %% Oszi-Plot
t = np.linspace(0, 50e-3, 100)
Up = 44.7 # in V
Ip = 2 # in A
w = 2 * np.pi / 20e-3
dt = 13.5e-3
u1 = Up * np.sin(w * t)
i1 = -Ip * np.sin(w * (t - dt))
fig = plt.figure(1)
ax1 = fig.add_subplot(111)
ax1.plot(t, u1, 'b-', label='u(t)')
ax1.set_ylabel('Spannung u/V')
ax1.set_xlabel('Zeit t/s')
ax1.set_ylim(-50, 50)
ax1.grid()
ax1.text(25e-3, 44.7, r'$\leftarrow$ 44.7 V')
# Zweite y-Achse fuer den Strom
ax2 = ax1.twinx()
ax2.plot(t, i1, 'r-', label='i(t)')
ax2.set_ylabel('Strom i/A')
ax2.set_ylim(-5, 5)
ax2.text(13.5e-3, 0, r'$\leftarrow$ 13.5 ms')
# ask matplotlib for the plotted objects and their labels
lines, labels = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax2.legend(lines + lines2, labels + labels2, loc=0)
plt.show()
An einem Verbraucher mit der Impedanz \(Z\) wird mittels eines Zweistrahloszilloskops eine zeitaufgelöste Strommessung des Stroms \(i(t)\) durchgeführt. Gleichzeitig wird die Klemmenspannung \(u(t)\) mit aufgenommen. Beide Zeitfunktionen sind sinusförmig. Ihre Amplituden und relativen Lagen sind der Abbildung 10.2 zu entnehmen.
Stellen Sie Strom und Spannung in reeller und komplexer Schreibweise dar.
\[ u(t) = \hat{U} \sin(\omega t); \quad \hat{U} = 44.7\,V \]
\[ i(t) = -\hat{I} \sin(\omega (t-\Delta t)); \quad \hat{I}=2\,A, \, \Delta t = 13.5\,ms \]
\[ u(t) = \hat{U} \cos\left(\omega t - \frac{\pi}{2} \right) \rightarrow \underline{U} = \frac{1}{\sqrt{2}} \hat{U}e^{-j\frac{\pi}{2}} \]
\[ i(t) = -\hat{I} \cos\left(\omega t- \omega\Delta t -\frac{\pi}{2}\right) \rightarrow \underline{I} = -\frac{1}{\sqrt{2}}\hat{I} e^{-j(\omega \Delta t + \frac{\pi}{2})} \]
Geben Sie für den Verbraucher die komplexe Leistung \(\underline{P}=P+jQ\) mit aufgenommener Wirkleistung \(P\) und aufgenommener Blindleistung \(Q\) an.
\[ \underline{P} = \underline{U} \cdot \underline{I}^* = -\frac{1}{2} \hat{U} \hat{I} e^{-j(\omega \Delta t)} = P + j Q \]
Koeffizientenvergleich:
\[ P = \operatorname{Re}\left\{\underline{P}\right\} = \operatorname{Re}\left\{-\frac{1}{2} \hat{U} \hat{I}e^{-j(\omega \Delta t)}\right\} = -\frac{1}{2} \hat{U} \hat{I}\cos(\omega \Delta t) = 20\,W \]
\[ Q = \operatorname{Im}\left\{\underline{P}\right\} = \operatorname{Im}\left\{-\frac{1}{2} \hat{U} \hat{I}e^{-j(\omega\Delta t)}\right\} = -\frac{1}{2} \hat{U} \hat{I}\sin(\omega \Delta t) = 40\,VA \]
Geben Sie eine Reihenschaltung und eine Parallelschaltung aus R-, L- und/oder C-Komponenten zur möglichen Realisierung des Verbrauchers an. Bestimmen Sie dazu die Komponentenwerte aus den gemessenen Strom- und Spannungsverläufen.
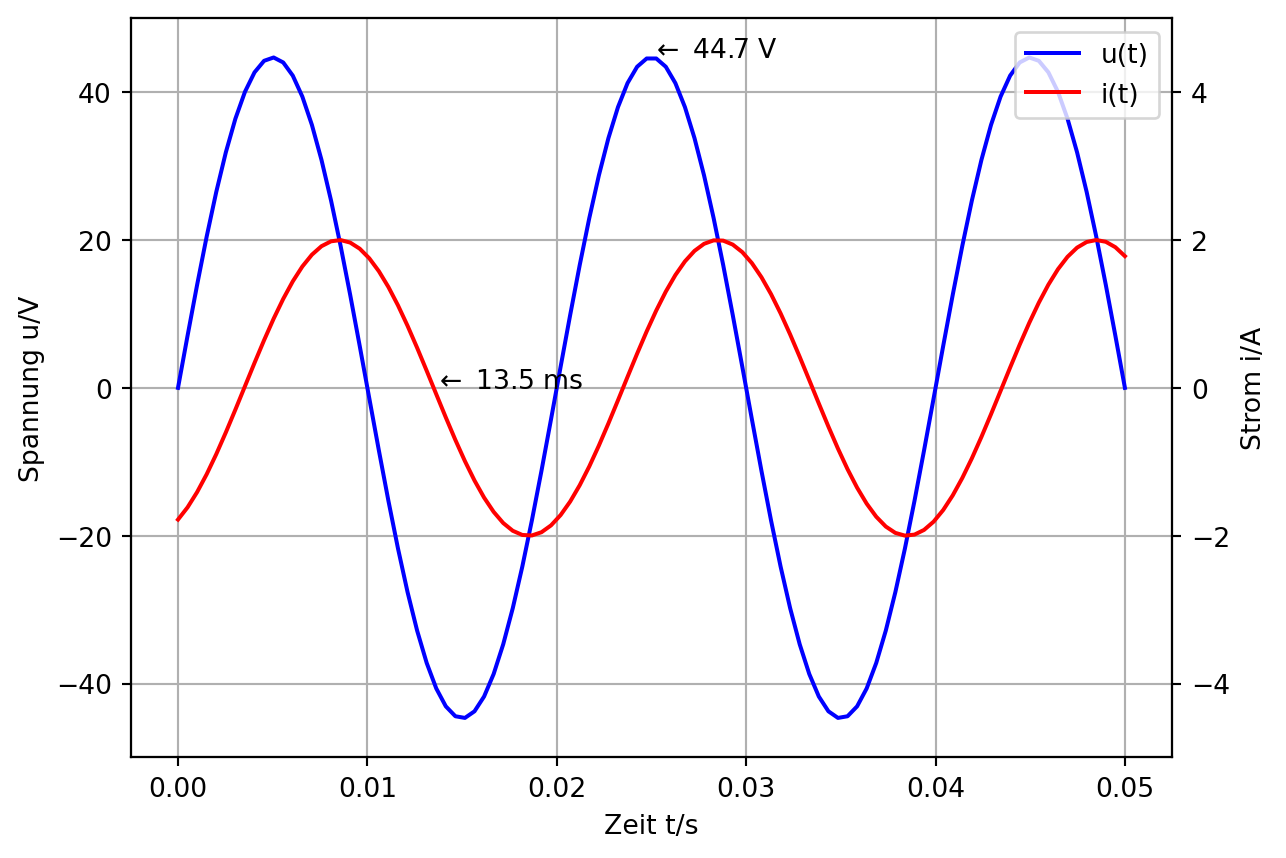
Reihen- oder Parallelschaltung aus Widerstand \(R\) und Induktivität \(L\). Für die Reihenschaltung errechnen sich die Bauteilwerte wie folgt:
\[\begin{align} Z &= \frac{\underline{U}}{\underline{I}} &= -\frac{\hat{U}}{\hat{I}}e^{j \omega \Delta t} &= (10 + j 20)\,\Omega &= R_s + j\omega L_s \end{align}\]
\[ R_s = 10\,\Omega \]
\[ L_s = \frac{20}{\omega}\,\Omega=640\,mH \]
Für die Realisierung mit einer Parallelschaltung, Umrechnen der Impedanzwerte in Admittanzwerte.
\[ Y = \frac{1}{R_p}+\frac{1}{j\omega L_p} = \frac{1}{Z} = \frac{1}{R_s+j \omega L_s} = \frac{R_s - j \omega L_s}{R_s^2+(\omega L_s)^2} \]
Ermittlung der Bauteilwerte für die Parallelschaltung durch Koeffizientenvergleich.
\[ \frac{1}{R_p} = \frac{R_s}{R_s^2+(\omega L_s)^2}; \quad R_p= 50\,\Omega \]
\[ \frac{1}{\omega L_p} = \frac{\omega L_s}{R_s^2+(\omega L_s)^2}; \quad \omega L_p = 25\,\Omega \]
\[ L_p = 796\,mH \]
