13  Periodische Signale

• Stromarten
• Kennwerte von Wechselgrößen

13.1 Stromarten

Neben dem Gleichstrom, der ausführlich in GEL1 behandelt wurde, gibt es weitere Stromarten.

Der Wechselstrom kennzeichnet sich durch sein beliebig periodisches Verhalten. Die Richtung und Größe variiert dabei mit der Zeit t. Eine Sonderform, die große Bedeutung hat ist der Sinusstrom.

Weiterhin gibt es den Mischstrom, der aus einer Überlagerung von Gleichstrom und Wechselstrom entsteht und zum Beispiel durch das Gleichrichten verursacht wird.

Des Weiteren gibt es noch die sogenannten modulierten Ströme. Dort schwanken entweder die Amplitude A, die Frequenz f oder der Nullphasenwinkel \(\varphi\) mit der Zeit t. Solche Signale werden hier nicht weiter behandelt. Diese kommen in dem Modul Grundlagen der Informationstechnik vor, welches im 4. Semester in der Vertiefungsrichtung Informationstechnik liegt.

import matplotlib.pyplot as plt

plt.figure()
plt.axhline(y = 0.75)
plt.xlabel('Zeit in s')
plt.ylabel('Spannung in V')
plt.title('Gleichstrom')
plt.grid()
plt.show()

import numpy as np
import matplotlib.pyplot as plt

T = 1
fs = 1000
time = np.linspace (0, T, T*fs)

f = 5
sinus1 = np.sin(2 * np.pi * f * time)
sinus2 = np.sin(2 * np.pi * 0.5*f * time)

plt.figure()
plt.plot(time,sinus1+sinus2)
plt.xlabel('Zeit in s')
plt.ylabel('Spannung in V')
plt.title('Wechselstrom')
plt.grid()
plt.show()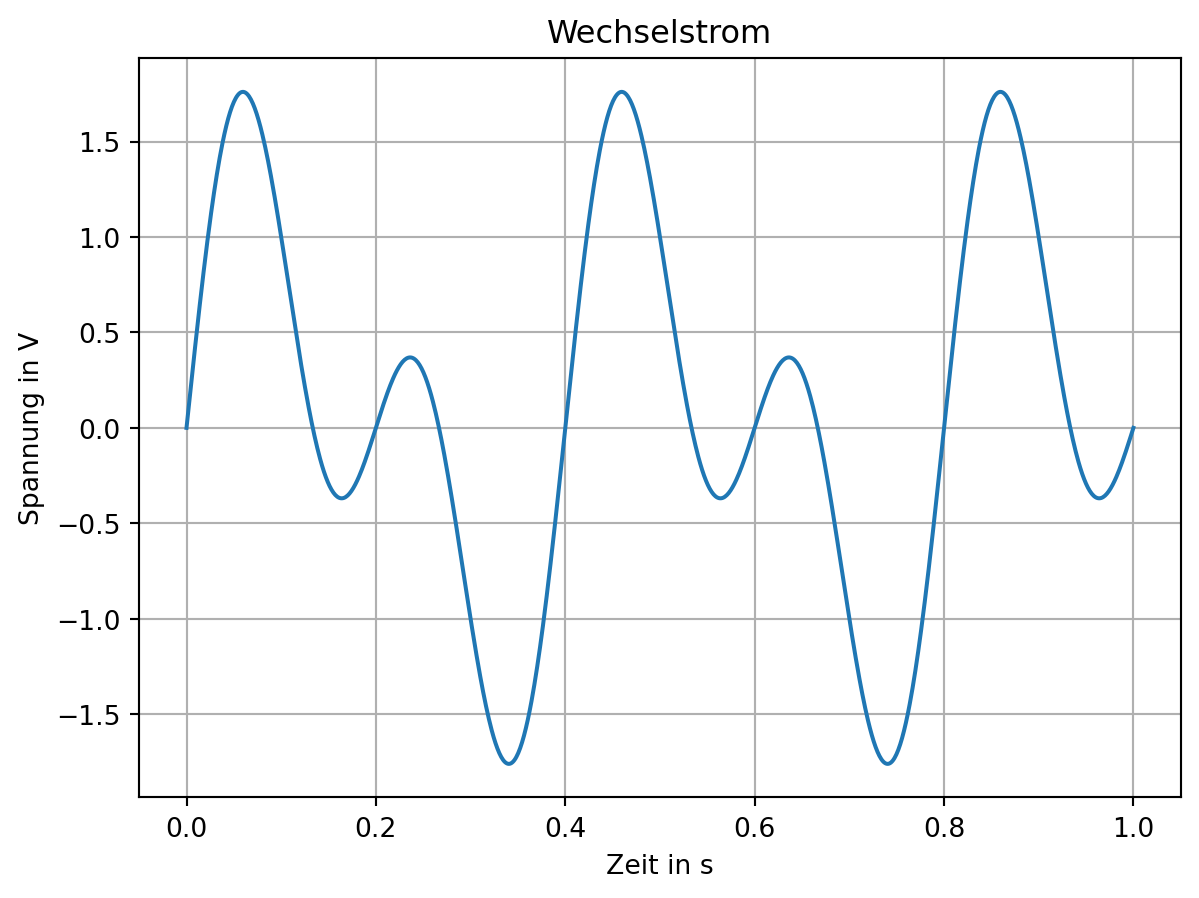

import numpy as np
import matplotlib.pyplot as plt

T = 1
fs = 1000
time = np.linspace (0, T, T*fs)

f = 5
sinus = np.sin(2 * np.pi * f * time)

plt.figure()
plt.plot(time,sinus)
plt.xlabel('Zeit in s')
plt.ylabel('Spannung in V')
plt.title('Sinusstrom')
plt.grid()
plt.show()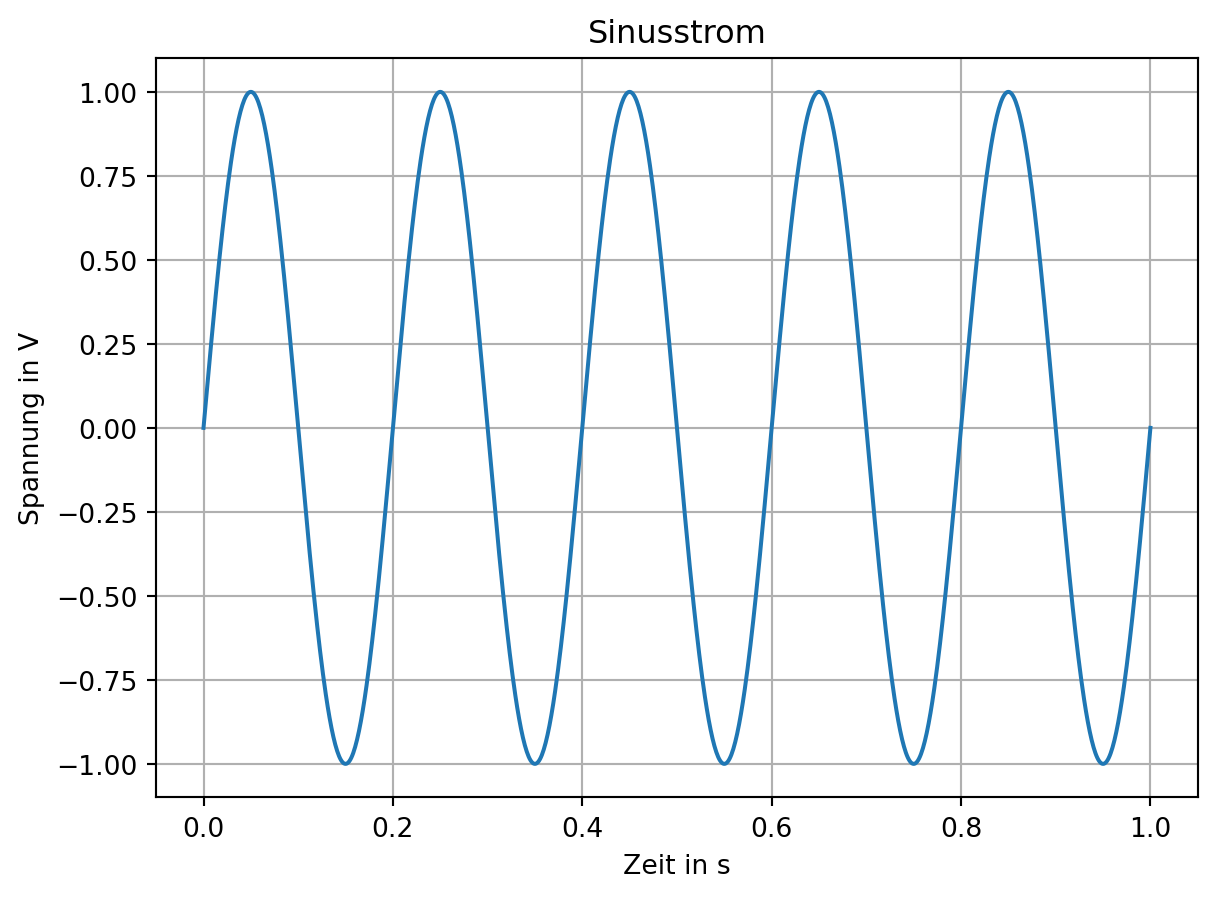

import numpy as np
import matplotlib.pyplot as plt

T = 1
fs = 1000
time = np.linspace (0, T, T*fs)

f = 5
sinus = np.sin(2 * np.pi * f * time)

plt.figure()
plt.plot(time,sinus+0.5)
plt.xlabel('Zeit in s')
plt.ylabel('Spannung in V')
plt.title('Mischstrom')
plt.grid()
plt.show()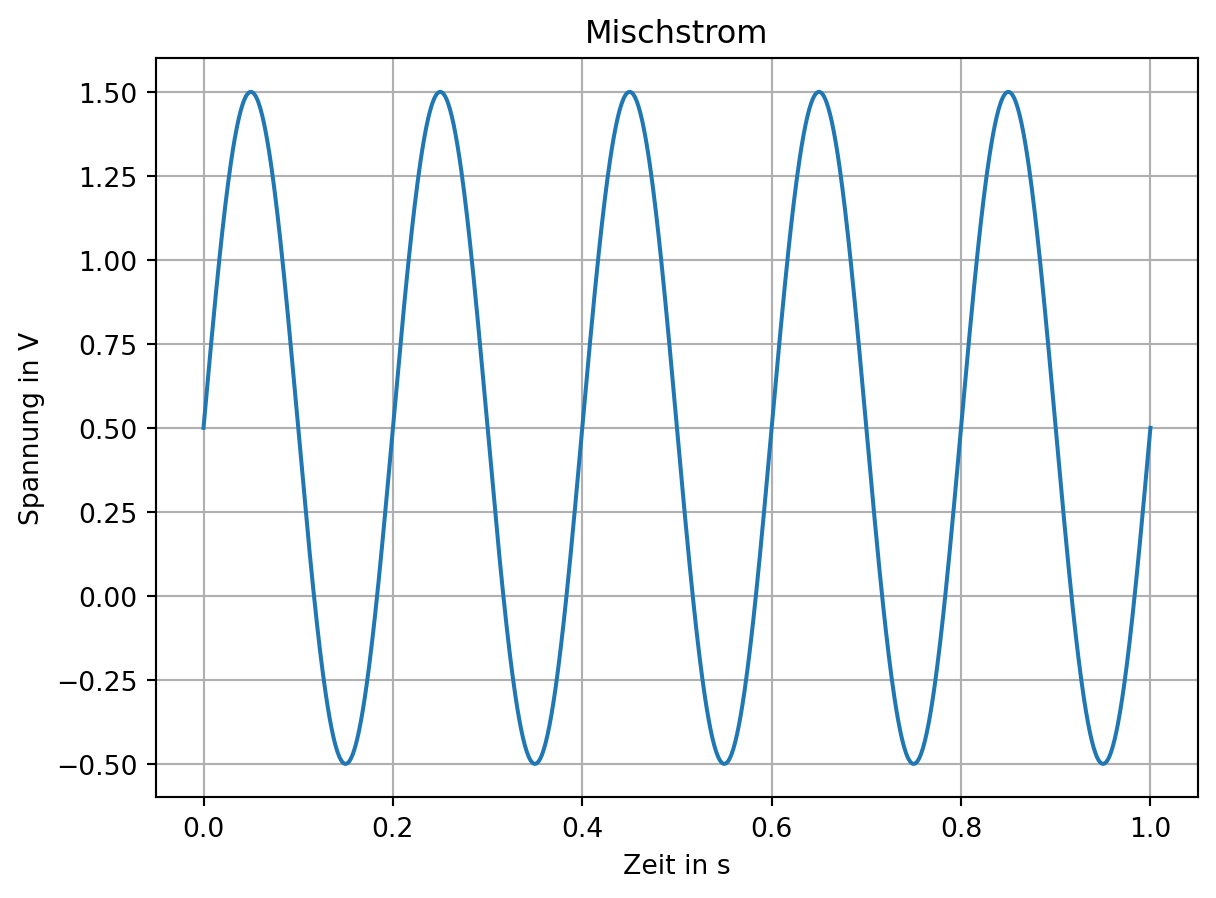

import numpy as np
import matplotlib.pyplot as plt

T = 1
fs = 1000
time = np.linspace (0, T, T*fs)

f = 20
sinus1 = np.sin(2 * np.pi * f * time)
sinus2 = 0.2 * np.sin(2 * np.pi * 0.1*f * time)
modulated = (1 + 0.5 * np.sin(2 * np.pi * 0.1*f * time)) * np.sin(2 * np.pi * f * time)

plt.figure()
plt.plot(time,modulated)
plt.xlabel('Zeit in s')
plt.ylabel('Spannung in V')
plt.title('amplituden-moduliertes Signal')
plt.grid()
plt.show()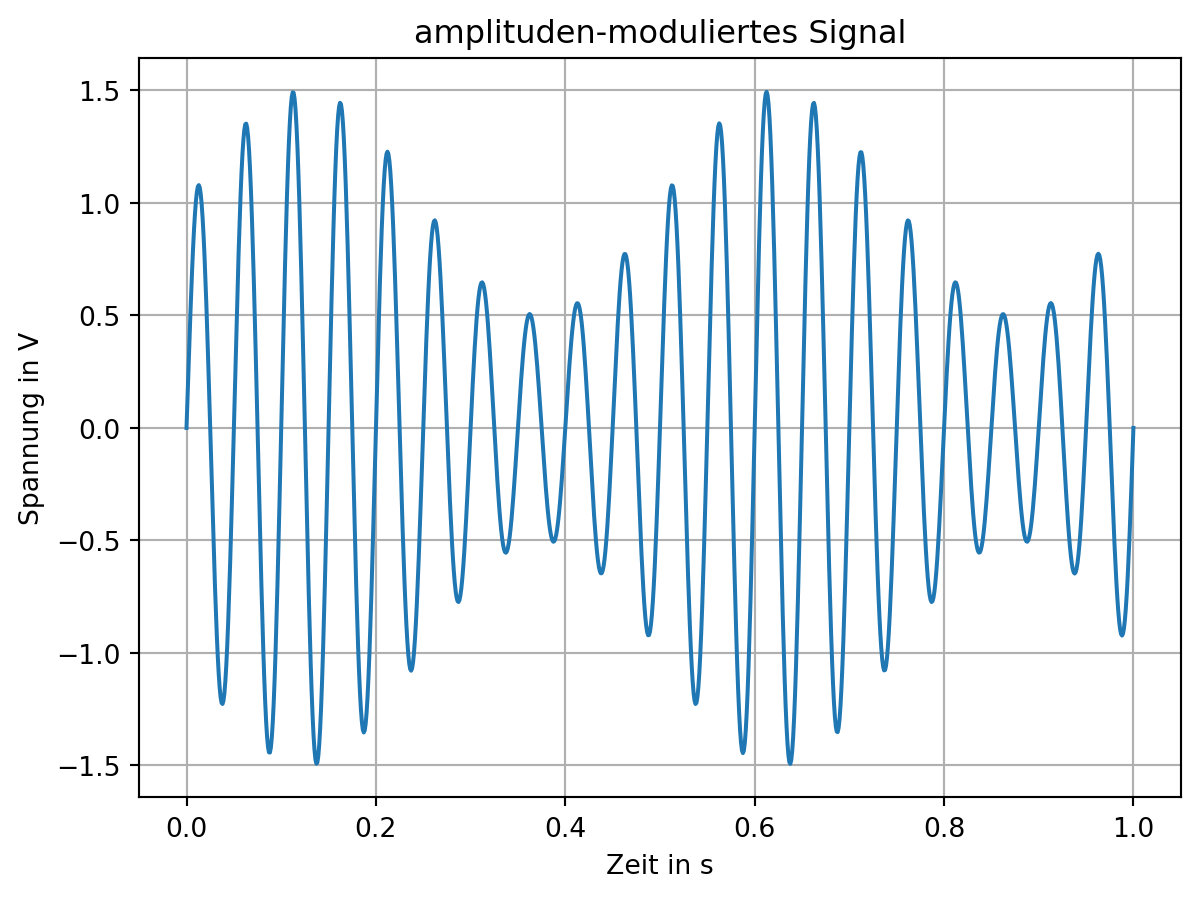

import numpy as np
import matplotlib.pyplot as plt

fs = 2000
fc = 100
fm = 15
beta = 3
t = np.arange(0,0.2,1/fs)

frm = np.cos(2*np.pi*fc*t + beta*np.sin(2*np.pi*fm*t))
m = np.cos(2*np.pi*fm*t)

plt.figure()
plt.plot(t,frm)
plt.xlabel('Zeit in s')
plt.ylabel('Spannung in V')
plt.title('frequenz-moduliertes Signal')
plt.grid()
plt.show()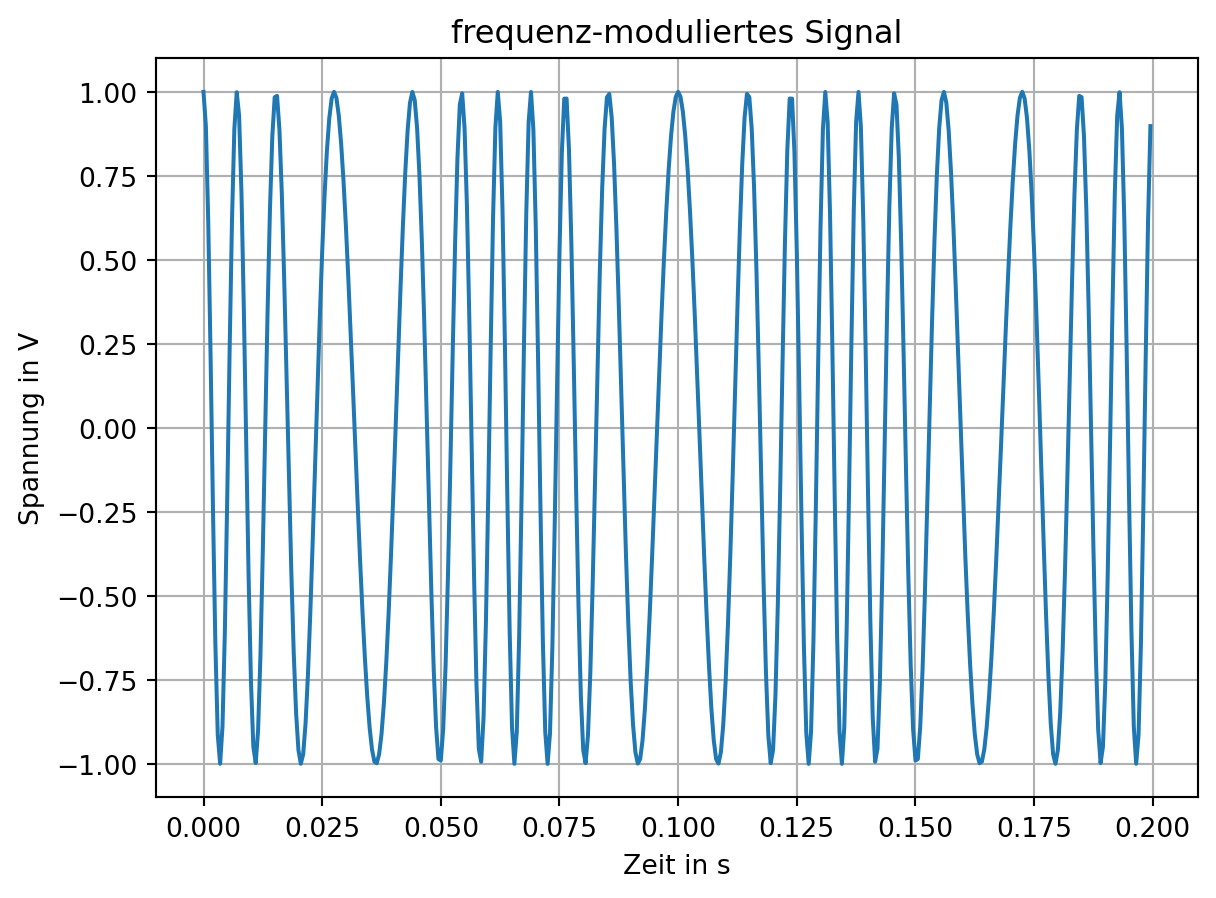

13.2 Kennwerte von Wechselgrößen

Allgemein kann man eine sich zeitlich ändernde sinusförmige Wechselgröße mit der folgenden Funktion beschreiben.

\[x = \hat{x} sin(\omega t + \varphi)\]

Dabei wird der Zeitwert x als auch der Scheitelwert \(\hat{x}\) mit einem kleinen Formelbuchstaben bezeichnet.

13.2.1 Periodendauer und Frequenz

Da sich eine sinusförmige Wechselgröße wiederholt sich nach Ablauf des Winkels \(2\pi = 360^° = \omega T\). Damit kann man die Periodendauer T über die Kreisfrequenz \(\omega\) darstellen.

\[T = \frac{2 \pi}{\omega}\]

Die Frequenz f gibt die Anzahl der Perioden pro Sekunde an und wird in Hz = 1/s gemessen. Die Frequenz ist der Kehrwert der Periodendauer.

\[f = \frac{1}{T}\]

Die Kreisfreqeunz ist die Frequenz mit dem Faktor \(2\pi\) erweitert. Sie wird in 1/s und nicht in Hz gemessen!

\[\omega = 2 \pi f = \frac{2\pi}{T}\]

13.2.2 Phasenlage

Sinusgrößen können zu verschiedenen Zeitpunkten ihre Scheitelwerte und Nulldurchgänge erreichen. Man sagt, dass diese Größen unterschiedliche Phasenlagen haben; sie sind gegeneinander phasenverschoben.

Abbildung 13.1

Entn. aus (Fricke und Vaske 1982)

13.2.2.1 Nullphasenwinkel

Allgemein gesprochen beginnt eine Sinusfunktion bei t=0 und geht um den Nullphasenwinkel \(\varphi_x\) früher als die normale Sinusfunktion \(sin(\omega t)\) durch Null. Das Vorzeichen des Winkel ist sehr wichtig!

Beim positiven Nulldurchgang der Sinusgröße wird ein Pfeil zum Nullpunkt gezeichnet. Ist der Pfeil in Zählrichtung der Zeitachse ist der Nullphasenwinkel positiv, ist der Pfeil entgegen der Zählrichtung der Zeitachse, dann ist er negativ (siehe Bild unter Phasenlage).

13.2.2.2 Phasenwinkel

Zusätzlich zum Nullphasewinkel gibt es den Phasenwinkel. Dieser gibt die Phasenverschiebung zwischen zwei Sinussignalen an. Es ist festgelegt, dass der Strom in solchen Fällen als Bezugsgröße genommen wird.

\[\varphi = \varphi_U - \varphi_I\]

Beispiel:

\[\varphi_I = -\frac{\pi}{3} = -60°\]

\[\varphi_U = \frac{\pi}{6} = 30°\]

\[\varphi = \varphi_U - \varphi_I = \left( \frac{\pi}{6} \right) - \left( -\frac{\pi}{3} \right) = 30° - (-60°) = \frac{\pi}{2} = 90°\]

Die Spannung eilt dem Strom um \(\varphi = 90°\) vor.

13.2.3 Mittelwert

Der Mittelwert ist der zeitlich durchschnittliche Wert einer Funktion.

\[\overline{x(t)} = \frac{1}{T} \int\limits_{t_0}^{t_o + T} x(t) dt\]

Bei reinem Wechselstrom ist der Mittelwert 0.

13.2.4 Gleichrichtwert

Der Gleichrichtwert ist der Mittelwert einer gleichgericheten Größe.

\[\overline{|x(t)|} = \frac{1}{T} \int\limits_{t_0}^{t_0 + T} |x(t)| dt\]

Verhältnis von Gleichricht- zu Scheitelwert (bei Sinusgrößen): \(\frac{\overline{|i|}}{\hat{i}} = 0.6366\)

13.2.5 Effektivwert

Der Effektivwert einer periodischen Spannung (oder eines periodischen Stroms) entspricht dem Wert einer Gleichspannung (eines Gleichstroms), der in einer ohmschen Last dieselbe Leistung umsetzt.

\[X = X_{eff} = \sqrt{\frac{1}{T} \int\limits_{t_0}^{t_0 + T} x^2(t) dt}\]

Scheitelfaktor

Der Scheitelfaktor ist das Verhältnis von Scheitelwert \(\hat{i}\) bzw. \(\hat{u}\) zum Effektivwert I bzw. U.

\[\xi = \frac{\hat{x}}{X_{eff}}\]

Der Scheitelfaktor für Sinusgrößen beträgt \(\xi = \sqrt{2} = 1.414\).

Der Scheitelfaktor für Dreieckspannung beträgt \(\xi = \sqrt{3}\).

Der Scheitelfaktor für Rechtecksignale beträgt \(\xi = 1\).

Formfaktor

Der Formfaktor stellt das Verhältnis von Effektivwert I bzw. U zu Gleichrichtwert \(\overline{|i|}\) bzw. \(\overline{|u|}\) dar.

\[F = \frac{X_{eff}}{\overline{|x|}}\]

Der Formfaktor für Sinusgrößen beträgt \(F = \frac{\pi}{2\sqrt{2}} \approx 1.11\).

Der Formfaktor für Dreiecksignale beträgt \(F = \frac{1.11}{2}\).

Der Formfaktor für Rechtecksignale beträgt \(F = 1.11\).

13.2.6 Effektivwert mit Gleichstromanteil

Abbildung 13.2

Entn. aus (Schenke 2023)

\[X_{eff} = \sqrt{X_o^2 + X_{eff\sim}^2}\]

13.3 Übungen

13.3.1 Aufgabe Gleichrichtwert

Ein Sinusstrom mit dem Scheitelwert \(\hat{i} = 10 A\) fließt durch die Gleichrichterschaltung-Brückenschaltung von Bild 3.4.

Abbildung 13.3

Entn. aus (Fricke und Vaske 1982)

Welche Elektrizitätsmenge Q wird während der Zeit t = 2 h befördert?
Tipp: \(Q = i \cdot t\)

Lösung

\[\overline{|i|} = 0.6366 \hat{i} = 0.6366 \cdot 10 A = 6.366 A\]

\[Q = \overline{|i|} t = 6.366 A \cdot 2 h = 12.73 Ah\]

13.3.2 Aufgabe Zeitfunktion berechnen

Die übliche Netzspannung 1982 betrug \(U = 220 V\) bei der Netzfrequenz \(f = 50 Hz\). Es sind der Gleichrichtwert \(\overline{|u|}\) und die Zeitfunktion u dieser Spannung zu bestimmen.

Lösung

Netzspannung ist Sinusförmig –> Formfaktor F = 1.111

Gleichrichtwert:

\[\overline{|u|} = \frac{U}{F} = \frac{220 V}{1.111} = 198 V\]

Zeitfunktion:

Scheitelwert:

\[\hat{u} = \sqrt{2} U = \sqrt{2} \cdot 220 V = 311.1 V\]

Kreisfrequenz:

\[\omega = 2 \pi f = 2 \pi \cdot 50 Hz = 314.2 \frac{1}{s}\]

\[u = \hat{u} sin(\omega t) = 311.1 V \cdot sin(314.2 1/s)\]

13.3.3 Aufgabe Mittelwerte aus Zeitverlauf bestimmen

Abbildung 13.4

Entn. aus (Albach und Fischer 2020)

Lösung 3.3

1. Mittelwert:

\[ \overline{u} = \frac{1}{T} \int\limits_{0}^{T} u(t)dt = \frac{1}{T} \left[ \hat{u} \frac{3T}{4} - \hat{u} \frac{T}{4} \right] = \frac{\hat{u}}{2} = 5 V \]

Gleichrichtwert:

\[ \overline{|u|} = \frac{1}{T} \int\limits_{0}^{T} |u(t)|dt = \frac{1}{T} \left[ \hat{u} \frac{3T}{4} + |-\hat{u}| \frac{T}{4} \right] = \hat{u} = 10 V \]

Effektivwert:

\[ U_{eff} = \sqrt{\frac{1}{T} \int\limits_{0}^{T} u^2(t)dt} = \sqrt{\frac{1}{T} \left[ \hat{u}^2 \frac{3T}{4} + (-\hat{u}^2) \frac{T}{4} \right]} = \hat{u} = 10 V \]

2. Mittelwert:

\[ \overline{u} = \frac{1}{T} \int\limits_{0}^{T} \hat{u} \frac{t}{T} dt = \frac{\hat{u}}{T^2} \frac{t^2}{2} \Big\vert_0^T = \frac{\hat{u}}{2} = 5 V \]

Gleichrichtwert:

\[\overline{|u|} = |u| = 5 V\]

Effektivwert:

\[ U_{eff} = \sqrt{\frac{1}{T} \int\limits_{0}^{T} \left(\hat{u} \frac{t}{T} \right)^2 dt} = \sqrt{\frac{\hat{u}^2}{T^3} \frac{t^3}{3} \Big\vert_0^T} = \sqrt{\frac{\hat{u}^2}{3}} = \frac{\hat{u}}{\sqrt{3}} = 5.77 V \]

3. Mittelwert:

\[\overline{u} = \frac{\hat{u}}{4} = 2.5 V\]

Gleichrichtwert:

\[\overline{|u|} = \overline{u} = 2.5 V\]

Effektivwert:

\[ U_{eff} = \sqrt{\frac{1}{T} \int\limits_{0}^{T/2} \left(2\hat{u} \frac{t}{T} \right)^2 dt} = \sqrt{\frac{4\hat{u}^2}{T^3} \frac{t^3}{3} \Big\vert_0^{T/2}} = \sqrt{\frac{\hat{u}^2}{6}} = \frac{\hat{u}}{\sqrt{6}} = 4.08 V \]

4. Mittelwert:

\[\overline{u} = 0 V\]

Gleichrichtwert:

\[\overline{|u|} = \frac{1}{T} \left[ \hat{u} \frac{T}{4} + \hat{u} \frac{T}{4} \right] = \frac{\hat{u}}{2} = 5 V\]

Effektivwert:

\[U_{eff} = \sqrt{\frac{1}{T} \int\limits_{0}^{T/2} \left( 2\hat{u} \frac{t}{T} \right)^2 dt + \frac{1}{T} \int\limits_{T/2}^{T} \left( 2\hat{u} \frac{t - T}{T} \right)^2 dt} = \sqrt{\frac{\hat{u}^2}{6} + \frac{\hat{u}^2}{6}} = \frac{\hat{u}}{\sqrt{3}} = 5.77 V\]

13.3.4 Aufgabe 3.4

Ein Wechselstrom besteht nach der Abbildung aus “angeschnittenen” Sinushalbschwingungen. In den Bereichen \(0 < \omega t < \alpha\) und \(\pi < \omega t < (\pi + \alpha)\) fließt kein Strom (i = 0), wobei \(\alpha = \pi/4 = 45°\) sei. In der übrigen Zeit (innerhalb des Bereiches \(0 < \omega t < 2\pi)\) wird der Stromverlauf durch die Gleichung \(i = \hat{i} sin(\omega t)\) wiedergegeben. Hierbei betrage der Scheitelwert des Stromes \(\hat{i} = 10 A\).

Wie groß ist der Effektivwert I des Stromes?

import numpy as np
import matplotlib.pyplot as plt

omega_t = np.arange(0,2*np.pi,np.pi/(2**6))
i = 10 * np.sin(omega_t)

alpha = np.pi/4

for a in range(len(i)):
    if omega_t[a] < alpha or (omega_t[a] > np.pi and omega_t[a] < np.pi+alpha):
        i[a] = 0
        
list_ticks = [None]*128
list_ticks[0] = '0'
list_ticks[63] = '$\pi$'
list_ticks[127] = '$2\pi$'
        
plt.figure()
plt.plot(omega_t, i)
plt.xlabel('$\omega t$')
plt.ylabel('i')
#plt.xticks([0,63,127],['0','$\pi$','2$\pi$'])
plt.xticks(omega_t,list_ticks)
plt.grid(True)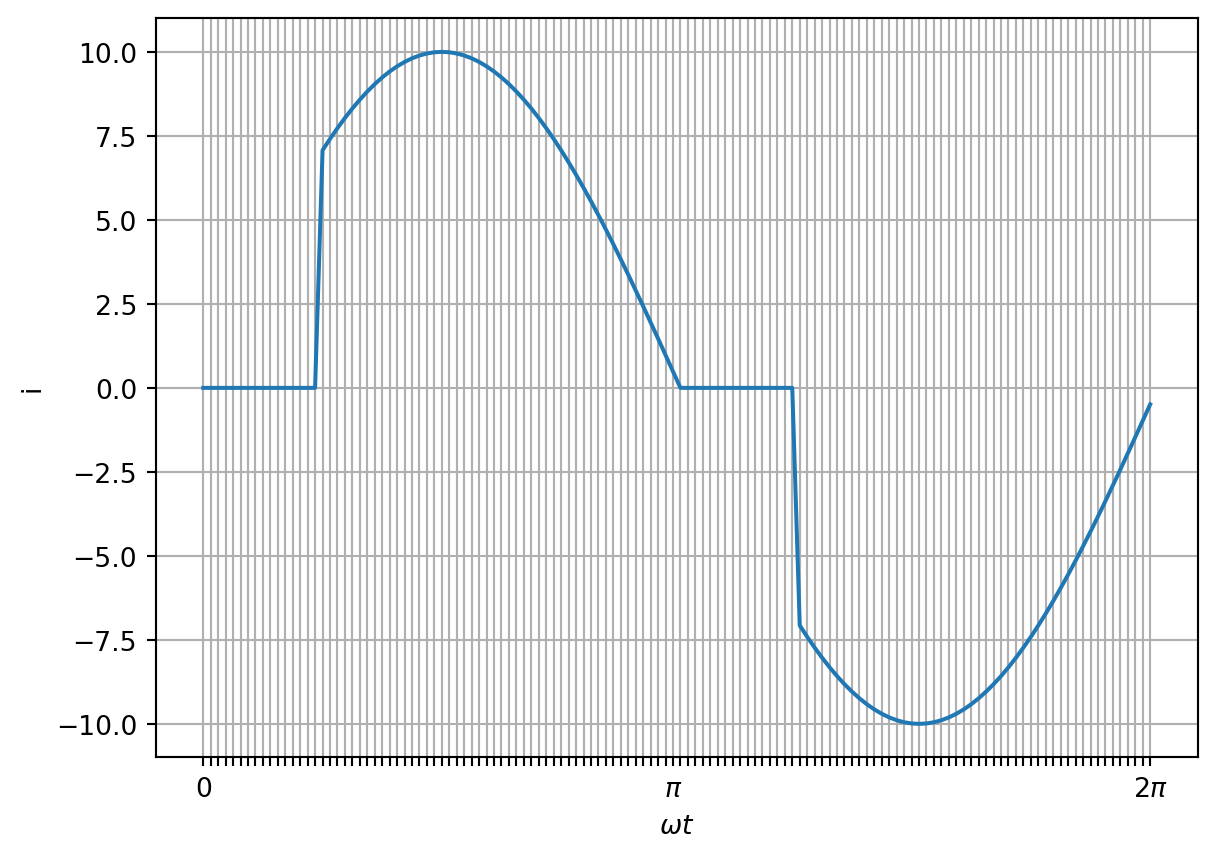

Lösung

\[I = \sqrt{\frac{1}{2\pi} \int\limits_{0}^{2\pi} i^2 d\omega t}\]

\[\int\limits_{0}^{2\pi} i^2 d\omega t = 2\int\limits_{0}^{\pi} i^2 d\omega t = 2\int\limits_{0}^{\pi} \hat{i}^2 \cdot sin^2(\omega t) d\omega t\]

\[2\int\limits_{0}^{\pi} \hat{i}^2 \cdot sin^2(\omega t) d\omega t = 2\hat{i}^2 \left(\frac{1}{2} \omega t - \frac{1}{4} sin(2\omega t) \right) \Big\vert_\alpha^\pi = \hat{i}^2 \left( \pi - \alpha + \frac{1}{2} sin(2\alpha) \right)\]

\[I = \sqrt{\frac{1}{2\pi} \cdot \int\limits_{0}^{2\pi} i^2 d\omega t} = \sqrt{\frac{1}{2\pi} \hat{i}^2 \left( \pi - \alpha + \frac{1}{2} sin(2\alpha) \right)} = \sqrt{\frac{1}{2\pi} \cdot (10 A)^2 \cdot \left( \pi - \frac{\pi}{4} + \frac{1}{2} \cdot sin(2 \cdot 45°) \right)} = 6.74 A\]

13.3.5 Aufgabe 3.5

An einem ohmschen Widerstand \(R = 30 \Omega\) liegt eine mittelwertfreie Dreieckspannung mit der Amplitude \(\hat{u} = 9 V\) und der Frequenz \(f = 100 Hz\) an.

Welche Wirkleistung P wird im zeitlichen Mittel im Widerstand R umgesetzt?

Lösung

Dreieckspannung –> Scheitelfaktor \(\xi = \sqrt{3}\)

\[U = \frac{\hat{u}}{\sqrt{3}} = \frac{9 V}{\sqrt{3}} = 5.196 V\]

\[P = \frac{U^2}{R} = \frac{5.196 V}{30 \Omega} = 0.9 W\]

13.3.6 Aufgabe 3.6

An einem ohmschen Widerstand R liegt eine Zägezahnspannung, die von einer Gleichspannung überlagert ist, an:

Abbildung 13.5

Entn. aus (Schenke 2023)

1. Bestimmen Sie den Mittelwert \(\overline{u(t)}\) des periodischen Spannungsverlaufes u(t).

2. Berechnen Sie den Effektivwert U des periodischen Spannungsverlaufes u(t).

3. Welche Wirkleistung P wird im zeitlichen Mittel im Widerstand R umgesetzt? (23.4)

Lösung

\[\overline{u(t)} = \frac{U_1 + U_2}{2}\]

\[U = \sqrt{\left( \frac{U_2 - U_1}{2 \cdot \sqrt{3}} \right)^2 + \left( \frac{U_1 + U_2}{2} \right)^2}\]

\[P = \frac{U^2}{R}\]

13.3.7 Aufgabe 3.7

Durch den ohmschen Widerstand R fließt ein Sinusstrom, der mit einem Gleichstrom überlagert ist:

Abbildung 13.6

Entn. aus (Schenke 2023)

1. Bestimmen Sie den Mittelwert \(\overline{i(t)}\) des periodischen Stromverlaufes i(t).

2. Berechnen Sie den Effektivwert I des periodischen Stromverlaufes i(t).

3. Welche Wirkleistung P wird im zeitlichen Mittel im Widerstand R umgesetzt? (23.6)

Lösung

\[\overline{i(t)} = I_0\]

\[I = \sqrt{I_0^2 + \left( \frac{I_0}{\sqrt{2}} \right)^2}\]

\[P = I^2 \cdot R\]

Albach, Manfred, und Janina Fischer. 2020. Elektrotechnik Aufgabensammlung. Pearson. https://elibrary.pearson.de/book/99.150005/9783863268930.

Fricke, H., und P. Vaske. 1982. Elektrische Netzwerke Grundlagen der Elektrotechnik 1. 17. Aufl. Stuttgart, Germany: B.G. Teubner.

Schenke, Stefan. 2023. „Grundlagen der Elektrotechnik — Jetzt schaffst Du die Prüfung!“ Helmut-Schmidt Universität Hamburg, Germany; online. http://www.stefan-schenke.de/get/.