1  Einleitung

1.1 Wissenschaftliches Rechnen / Datenwissenschaft

1.2 EDA Tools

1.3 Betriebssystem (OS) - Werkzeuge (Tools)

1.4 Code Editoren

1.5 Berichtswesen / Laborberichte

1.6 Schöne neue Welt

AMD Jaguar APU (CPU/GPU), 16 nm, 325 qmm, 2016

1.7 Halbleiterherstellung (Infineon, Dresden)

1.8 FinFET (Intel)

1.9 TSMC Fab (Next Gen 7/5 nm)

1.10 Es war einmal …

1906 die Elektronenröhre

1947 der erste Transistor, Bell Labs Foto

1.11 Damals und heute

1958 Jack Kilby’s erster IC

Moderner IC

1.12 Systemhierarchie

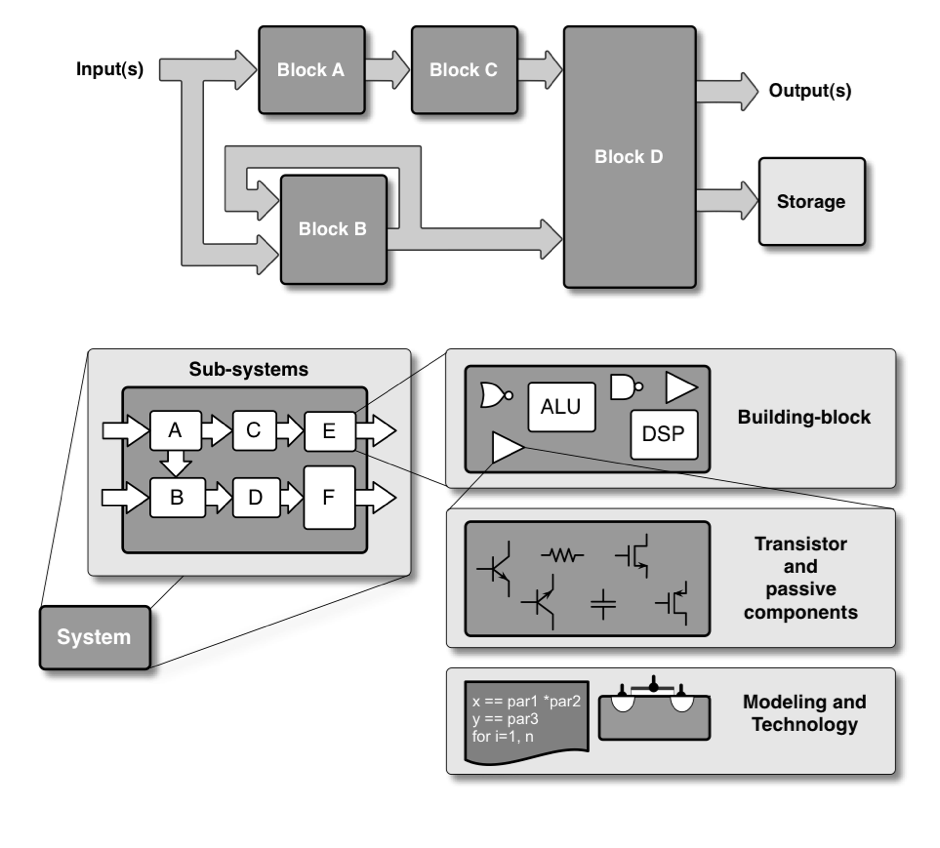
Funktionsblöcke eines elektronischen Systems

  • Nutzen Sie Hierarchien zur Beschreibung komplexer Systeme

  • Teile und herrsche

1.13 Schnittstellen zur Aussenwelt

Interfacing

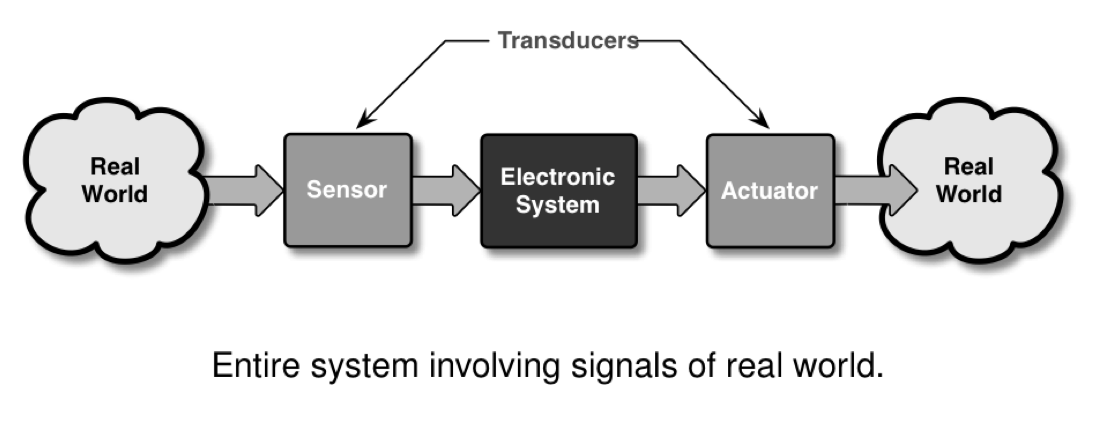
1.14 Meeting mit einem System

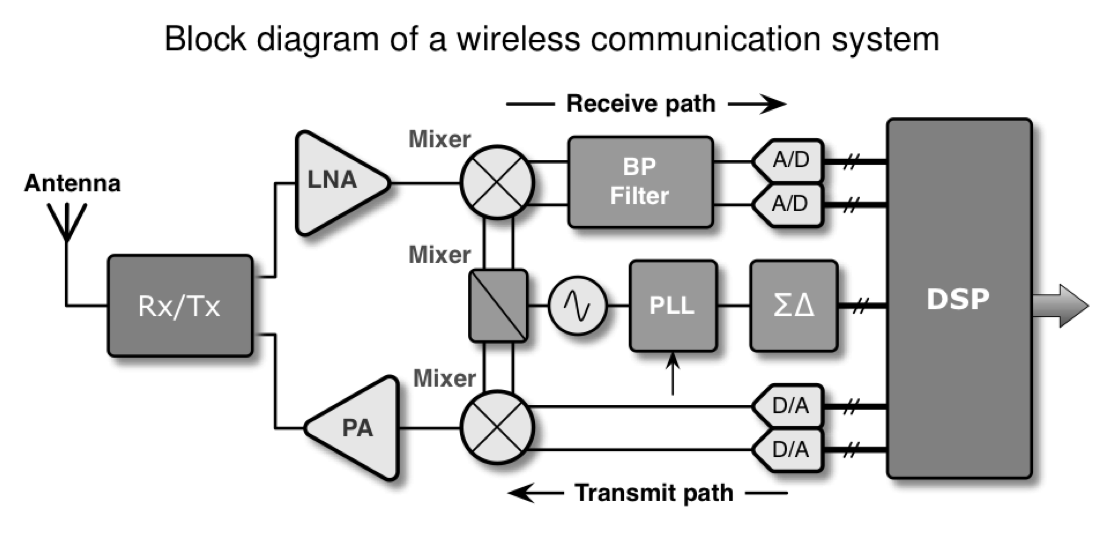
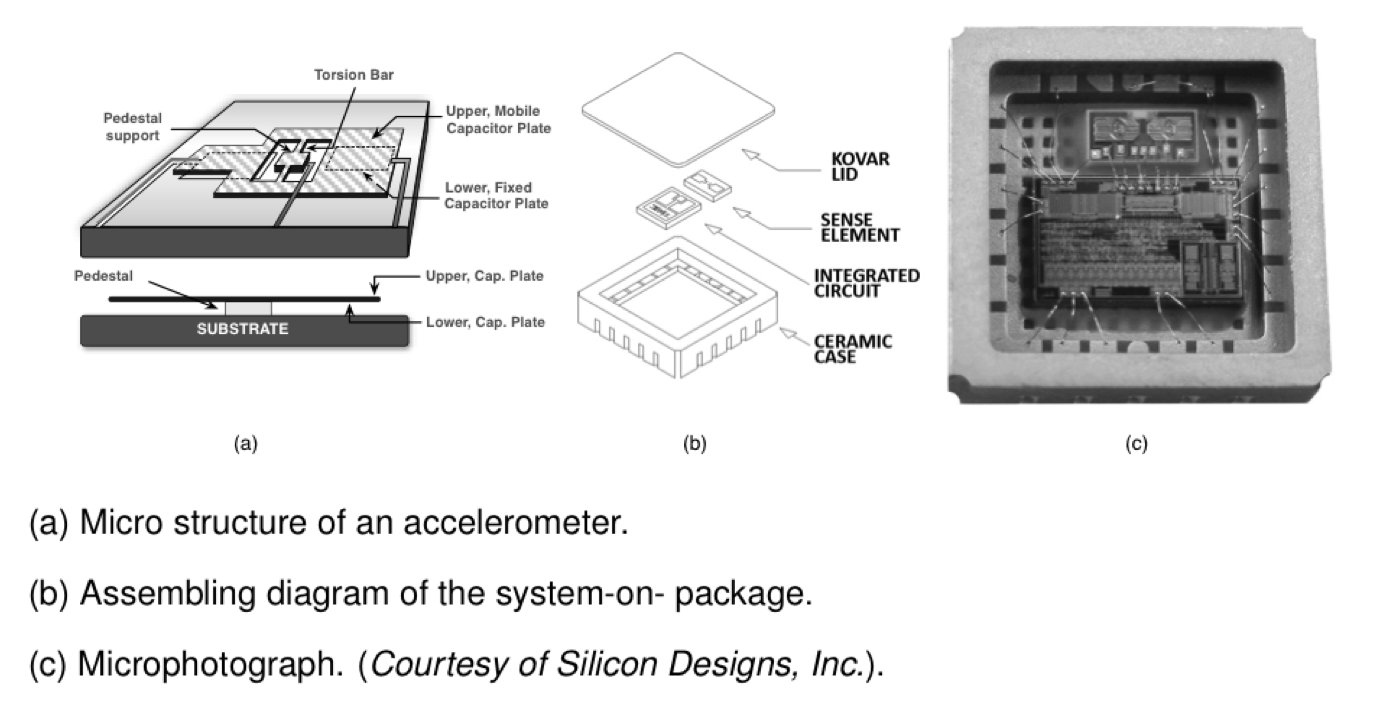
Drahtloses Kommunikationssystem

1.15 System in a Package (SiP)

Beschleunigungssensor

1.16 Sie werden unsere Experten

  • Hintergrundwissen

    • Systemverständnis, Architektur, Herstellungsverfahren, Implementation

  • Unterbewusste Kompetenz

    • Abgespeicherte Erfahrungen aus Erfolgsgeschichten und Misserfolgen

  • Spezialwissen

    • Berufsspezifisches Wissen

  • Teamwork Haltung

    • Kommunikationsfähigkeit, Berichtswesen und technische Präsentation

  • Kreativität

  • Tool-Kenntnisse

1.17 Lernziele des Moduls

  • Elektrische Systeme mathematisch und graphisch im Zeit- und Frequenzbereich beschreiben

  • Netzwerkanalyse mit RLC-Gliedern

  • Spezielle Netzwerke, wie Messbrücken, Schwingkreise und ideale Transformatoren, dimensionieren.

1.18 Seminaristischer Unterricht

  • Komplexe Wechselstromrechnung

  • Diskrete Bauelemente und ihre Modellierung (RLC)

  • Methodik der Netzwerkanalyse

  • Anwendungsbeispiele mit EDA-Werkzeugen und wissenschaftliches Rechnen (Scientific Computing)

1.19 Beschreibung elektrotechnischer Systeme

  • verschiedene Stufen der Vereinfachung

  • Felder / Wellen / Optik / HF-Technik

    • Maxwell-Gleichungen \[\begin{align} \oint \mathbf{H} d\mathbf{s} &= \iint \mathbf{J} + \dot{D} d\mathbf{A} \\ \oint \mathbf{E} d\mathbf{s} &= - \iint \dot{B} d\mathbf{A} \end{align}\]

  • bei lokaler Konzentration der Feldenergie \(\Rightarrow\) quasi-statische Näherung

  • Mikrowellentechnik / Leitungstechnik

    • verteilte Schaltungen \(l\), \(c\), \(\rho\)

    • Kopplung, Laufzeit \(\tau = a/v\)

  • kleine Systeme mit \(a << \lambda\) bzw. kurze Laufzeiten mit \(\tau << T\)

  • Regelungstechnik / Impulstechnik

    • Ersatzschaltungen

    • (Block-)Schaltbilder

  • eingeschwungener Zustand

  • NF-Technik

    • stationär-periodische Signale

  • Sinussignale

  • Energietechnik

    • monofrequente Signale \(\underline{U} = \underline{Z} \cdot \underline{I}\)

  • Frequenz \(f \rightarrow 0\)

  • Gleichstromtechnik

    • Ohmsches Gesetz \(U = R \cdot I\)

1.20 Konzentrierte Schaltelemente

HinweisStromdichte

\[ \frac{\int E(r,t) ds}{\iint J(r,t) dA} = \frac{u(t)}{i(t)} \Rightarrow R \]

HinweisVerschiebungsdichte

\[ \frac{\iint D(r,t) dA}{\int E(r,t) ds} = \frac{q(t)}{u(t)} \Rightarrow C \]

HinweisFlußdichte

\[ \frac{\iint B(r,t) dA}{\oint H(r,t) ds} = \frac{u(t)}{i(t)} \Rightarrow L \]

1.21 Harmonische Signale

Hinweisals Zeitfunktion

\[ u(t) = \hat{u} \sin(\omega t + \varphi) \]

Hinweisals Zeiger / komplexe Grösse (Phasor)

\[ \underline{\hat{u}} = \\hat{u} e^{j \varphi} \]