16 Komplexe Zahlen
16.1 Die imaginäre Einheit
Die imaginäre Einheit \(j\) ist definiert als:
\[j^2 = -1\]
Für höhere Potenzen von \(j\) erhält man:
\[j^2 = -1\]
\[j^3 = -j\]
\[j^4 = 1\]
\[j^5 = j\]
\[j^6 = -1\]
usw.
16.2 Aufbau komplexer Zahlen
Komplexe Zahlen bestehen aus einem Real- und einem Imaginärteil. Sie werden durch einen Unterstrich gekennzeichnet. Ist der Buchstabe nicht unterstrichen, wird von dem Betrag der komplexen Zahl geredet.
\[\underline{Z} = \operatorname{Re}\{\underline{Z}\} + j \cdot \operatorname{Im}\{\underline{Z}\}\]
In der Elektrotechnik wird zur Kennzeichnung des Imaginärteils oft der Buchstabe \(j\) anstelle des \(i\) verwendet, da das \(i\) für die Bezeichnung des Stromes vorgesehen ist.
16.3 Rechenoperationen
16.3.1 Addition von komplexen Zahlen
Zwei Komplexe Zahlen \(\underline{Z}_1\) und \(\underline{Z}_2\) werden addiert, indem ihre Real- und Imaginärteile getrennt voneinander addiert werden.
\[ \underline{Z}_1 + \underline{Z}_2 = \operatorname{Re}\{\underline{Z}_1\} + \operatorname{Re}\{\underline{Z}_2\} + j(\operatorname{Im}\{\underline{Z}_1\} + \operatorname{Im}\{\underline{Z}_2\}) \]
16.3.2 Subtraktion von komplexen Zahlen
Zwei Komplexe Zahlen \(\underline{Z}\) und \(\underline{Z}_2\) werden subtrahiert, indem ihre Real- und Imaginärteile getrennt voneinander abgezogen werden.
\[ \underline{Z} - \underline{Z}_2 = \operatorname{Re}\{\underline{Z}\} - \operatorname{Re}\{\underline{Z}_2\} + j(\operatorname{Im}\{\underline{Z}\} - \operatorname{Im}\{\underline{Z}_2\}) \]
16.3.3 Betrag einer komplexen Zahl
Der Betrag einer komplexen Zahl \(\underline{Z}\) ist die Euklidische Länge des Vektors, wenn dieser zum Beispiel in einem Koordinatensystem gezeichnet ist. Der Betrag wird als \(|\underline{Z}|\) oder vereinfacht als A geschrieben.
\[ A = |\underline{Z}| = \sqrt{\operatorname{Re}\{\underline{Z}\}^2 + \operatorname{Im}\{\underline{Z}\}^2} \]
16.3.4 Phasenwinkel einer komplexen Zahl
\[ \varphi = arctan\left(\frac{\operatorname{Im}\{\underline{Z}\}}{\operatorname{Re}\{\underline{Z}\}}\right) \]
Der Phasenwinkel wird überlicherweise von 0° bis 180° positiv (Zählweise CCW) und von 180° bis 360° negativ (Zählweise CW) angegeben.
16.3.5 Eulersche Identität und Polarkoordinaten
Komplexe Zahlen können auch als Polarkoordinaten über die Eulersche Identität beschrieben werden. Dabei setzt sich das aus Betrag und Phasenwinkel zusammen.
\[ \underline{Z} = \operatorname{Re}\{\underline{Z}\} + j \cdot \operatorname{Im}\{\underline{Z}\} = A \cdot e^{j\varphi} \]
16.3.5.1 Eulersche Identität
\[ e^{j\varphi} = cos(\varphi) + j \cdot sin(\varphi) \]
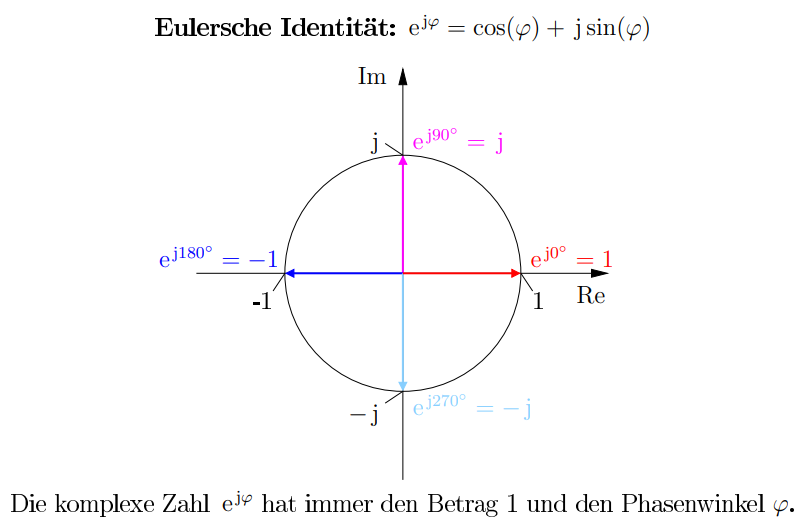
Die komplexe Zahl \(e^{j\varphi}\) hat immer den Betrag 1 und den Phasenwinkel \(\varphi\).
16.3.6 Multiplikation komplexer Zahlen
Die Multiplikation ist über die Polarkoordinaten einfacher. Bei der Multiplikation werden die Beträge multipliziert und die Phasenwinkel addiert.
\[ \underline{Z} \cdot \underline{Z}_2 = Z_1 \cdot Z_2 \cdot e^{j(\varphi_{Z_1} + \varphi_{Z_2})} \]
16.3.7 Division komplexer Zahlen
Ähnlich zur Multiplikation werden bei der Division die Beträge dividiert und die Phasenwinkel subtrahiert.
\[ \frac{\underline{Z}_1}{\underline{Z}_2} = \frac{Z_1}{Z_2} \cdot e^{j(\varphi_{Z_1} - \varphi_{Z_2})} \]
16.3.8 Kehrwert einer komplexen Zahl
Beim Kehrwert einer komplexen Zahl wird der Kehrwert des Betrages genommen und das Vorzeichen des Phasenwinkels invertiert.
\[ \frac{1}{\underline{Z}} = \frac{1}{Z} \cdot e^{-j\varphi} \]
16.3.9 Konjugiert-Komplex
Beim konjugiert-komplexen einer Zahl wird das Vorzeichen des Imaginärteils invertiert, dadurch verändert sich der Betrag nicht, aber der Phasenwinkel wird invertiert.
\[\underline{Z} = \operatorname{Re}\{\underline{Z}\} + j \cdot \operatorname{Im}\{\underline{Z}\}\]
\[\underline{Z}^* = \operatorname{Re}\{\underline{Z}\} - j \cdot \operatorname{Im}\{\underline{Z}\}\]
16.4 Übungen
Aufgabe 2.1
\(\sqrt{-9} + \sqrt{-x^2} - \sqrt{-y^2} + \sqrt{-25}\)
\[3\sqrt{-1} + x\sqrt{-1} - y\sqrt{-1} + 5\sqrt{-1} = j3 + jx - jy + j5 = j(8 + x - y)\]
Aufgabe 2.2
\(\frac{3 j^3 \cdot 5 j^4}{6 j^{20}}\)
\(\frac{1}{j^5} + \frac{1}{j^7}\)
\[\frac{-j3 \cdot 5}{6 i^4} = \frac{-j15}{6} = -j2,5\]
\[\frac{1}{j} + \frac{1}{-j} = -j + j = 0\]
Aufgabe 2.3
\((1 + 2j) - (-2 + 3j) + (-3 + j) - (5 + 4j) - (-1 + 9j) + (5 - 8j)\)
\((-2a + 3j) - (u - uj) + (-2a -3j) - (-u - vj)\)
1 - j21
-4a + j(u + v)
Aufgabe 2.4
\((5 - 2j)(-3 + j)\) (Ergebnis in kartesischer Form)
\(\left(3\sqrt{2} + 5\sqrt{3}j\right)\left(3\sqrt{2} - 5\sqrt{3}j\right)\) (Ergebnis in kartesischer Form)
-13 + j11
93
Aufgabe 2.5
\(\frac{3 + 4j}{2 + j}\)
\(\frac{1}{\sqrt{5} - j}\)
\(\frac{3j}{1 - j}\)
\(\frac{(3 + 4j)(2 - j)}{(2 + j)(2 - j)} = \frac{6 + 8j - 3j + 4}{4 + 1} = 2 + j\)
\(\frac{1(\sqrt{5} + j)}{(\sqrt{5} - j)(\sqrt{5} + j)} = \frac{\sqrt{5} + j}{5 + 1} = \frac{\sqrt{5}}{6} + j\frac{1}{6}\)
\(\frac{3j(1 + j)}{(1 - j)(1 + j)} = \frac{-3 + 3j}{1 + 1}= -\frac{3}{2} + j\frac{3}{2}\)
Aufgabe 2.6
\(\frac{1 + j}{1 - j} + \frac{1 - j}{1 + j}\)
\(\frac{1 - j}{1 + j} - \frac{1 + j}{1 - j}\)
\(\frac{1 + j}{1 - j} + \frac{1 - j}{1 + j} = \frac{(1 + j)^2 + (1 - j)^2}{(1 - j)(1 + j)} = \frac{1 + 2j - 1 + 1 -2j - 1}{1 + 1} = 0\)
\(\frac{(1 - j)^2 - (1 + j)^2}{(1 + j)(1 - j)} = \frac{1 - 2j - 1 - (1 + 2j - 1)}{1 + 1} = \frac{-4j}{2} = -2j\)
Aufgabe 2.7
In die Exponentialform umwandeln:
\(0,5 - \sqrt{6}j\)
\(\sqrt{3} + \sqrt{3}j\)
3 - 2j
\(2,5 \cdot e^{j \cdot 4,914}\)
\(2,45 \cdot e^{j \cdot \frac{\pi}{4}}\)
\(3,61 \cdot e^{j \cdot 5,695}\)
Aufgabe 2.8
In die arithmetische Form umwandeln:
\(83 e^{j \cdot 1,1083}\)
\(3,8 e^{-j \cdot 5,524}\)
\(e^{0,2 + 1,2j}\)
\(83(cos(1,1083) + j sin(1,1083)) = 37,03 + j74,28\)
\(3,8(cos(-5,524) + j sin(-5,524)) = 2,757 + j2,616\)
\(e^{0,2}(cos(1,2) + j sin(1,2)) = 0,443 + j1,138\)
Aufgabe 2.9
Für \(z_1 = 1,5 - 0,5j\) und \(z_2 = 3 + 0,5j\) die Exponentialform berechnen und die folgende Gleichung in der arithmetischen Form angeben:
\[z = \frac{z_1 \cdot z_2}{z_1 + z_2}\]
\[z_1 = \frac{\sqrt{10}}{2} \cdot e^{-j \cdot 0,322}\]
\[z_2 = \frac{\sqrt{37}}{2} \cdot e^{j \cdot 0,165}\]
\[z_1 + z_2 = 4,5\]
\[\frac{\frac{\sqrt{370}}{4} \cdot e^{j(-0,322 + 0,165)}}{4,5} = 1,069 \cdot e^{-j 0,157} = 1,056 - j0,167\]
Aufgabe 2.10
Bringe den folgenden Term in die Darstellung \(\underline{Z} = \operatorname{Re}\{\underline{Z}\} + j \cdot \operatorname{Im}\{\underline{Z}\}\):
\[\frac{\frac{1}{j\omega C}}{R + \frac{1}{j\omega C}}\]
\[ \frac{1}{j\omega RC} = \frac{1 - j\omega RC}{(1 + j\omega RC)(1- j\omega RC)} = \frac{1}{1 + (\omega RC)^2} - j\frac{\omega RC}{1 + (\omega RC)^2} \]
Aufgabe 2.11
Bringe den folgenden Term in die Darstellung \(\underline{Z} = \operatorname{Re}\{\underline{Z}\} + j \cdot \operatorname{Im}\{\underline{Z}\}\):
\[\frac{\frac{1}{j\omega C}}{j\omega L + R + \frac{1}{j\omega C}}\]
\[ \frac{1}{- \omega^2 LC + j\omega RC + 1} = \frac{1 - \omega^2 LC - j\omega RC}{(1 - \omega^2 LC)^2 + (\omega RC)^2} = \frac{1 - \omega^2 LC}{(1 - \omega^2 LC)^2 + (\omega RC)^2} - j\frac{\omega RC}{(1 - \omega^2 LC)^2 + (\omega RC)^2} \]