10. Klausurvorbereitung

Aufgabe 11.1 (Übertragungsfunktion)

(Weißgerber Klausursammlung Abschnitt 3 Aufgabenblatt 1 Aufagbe 1.1)

[Weißgerber, 2015]

Ermitteln Sie das Spannungsverhältnis \(\frac{\underline{U}_2}{\underline{U}_1}\). Die Hilfsspannung \(\underline{U}_h\) soll die Lösung erleichern.

Lösung 11.1

\[\frac{\underline{U}_2}{\underline{U}_1} = \frac{\underline{U}_2}{\underline{U}_h} \cdot \frac{\underline{U}_h}{\underline{U}_1}\]

\[\frac{\underline{U}_2}{\underline{U}_h} = \frac{\frac{1}{j\omega C}}{R + \frac{1}{j\omega C}}\]

\[\frac{\underline{U}_2}{\underline{U}_1} = \frac{\frac{\left( R + \frac{1}{j\omega C}\right)\cdot \frac{1}{j\omega C}}{R + \frac{2}{j\omega C}}}{\frac{\left( R+ \frac{1}{j\omega C}\right)\cdot \frac{1}{j\omega C}}{R + \frac{2}{j\omega C}} + R} = \frac{\left( R + \frac{1}{j\omega C}\right) \cdot \frac{1}{j\omega C}}{\left( R + \frac{1}{j\omega C}\right)\cdot \frac{1}{j\omega C} + R \cdot \left( R + \frac{2}{j\omega C}\right)}\]

\[\frac{\underline{U}_2}{\underline{U}_1} = \frac{\frac{1}{j\omega C}}{R + \frac{1}{j\omega C}} \cdot \frac{\left( R + \frac{1}{j\omega C}\right) \cdot \frac{1}{j\omega C}}{\left( R + \frac{1}{j\omega C}\right)\cdot \frac{1}{j\omega C} + R \cdot \left( R + \frac{2}{j\omega C}\right)}\]

\[\frac{\underline{U}_2}{\underline{U}_1} = \frac{\left( \frac{1}{j\omega C}\right)^2}{\left(R + \frac{1}{j\omega C}\right)\cdot \frac{1}{j\omega C} + R \cdot \left( R + \frac{2}{j\omega C}\right)^2}\]

\[\frac{\underline{U}_2}{\underline{U}_1} = \frac{1}{R \cdot j\omega C + 1 + R^2 \cdot (j\omega C)^2 + 2\cdot R\cdot j\omega C}\]

\[\frac{\underline{U}_2}{\underline{U}_1} = \frac{1}{(1 - \omega^2 R^2 C^2) + j\omega 3RC}\]

Aufgabe 11.2 (Schwingkreis)

(Weißgerber Klausursammlung Abschnitt 3 Aufgabenblatt 4 Aufgabe 2)

[Weißgerber, 2015]

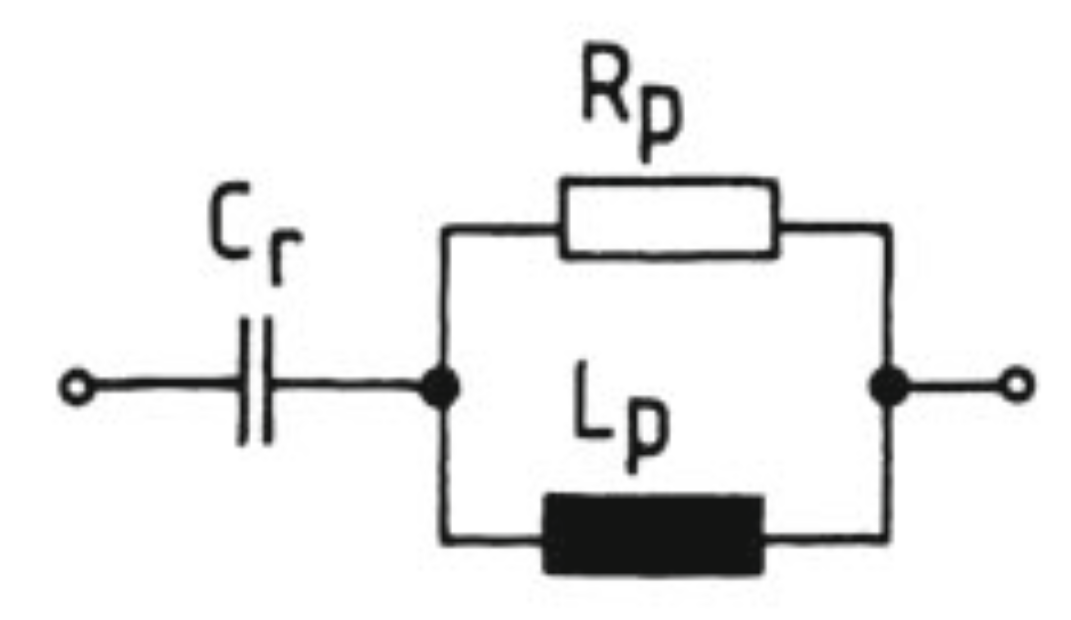
a) Entwickeln Sie die Formel für den komplexen Widerstand \(\underline{Z}\) der gezeichneten Schaltung in algebraischer Form (Real- und Imaginärteil soll getrennt sein).

b) Berechnen Sie den Wert der Induktivität \(L_p\), damit bei gegebenen Größen \(C_r = 2\,\mu F\), \(R_p = 1\,k\Omega\) und \(\omega = 1000 s^{-1}\) die Schaltung in Resonanz ist.

c) Kontrollieren Sie das Ergebnis für \(L_p\), indem Sie den komplexen Widerstand \(\underline{Z}\) berechnen.

Lösung 11.2

a)

Aufstellen der Gleichung und konjugiert-komplex erweitern:

\[\underline{Z} = \frac{1}{j\omega C_r} + \frac{1}{\frac{1}{R_p} + \frac{1}{j\omega L_p}} = -j \cdot \frac{1}{\omega C_r} + \frac{1}{\frac{1}{R_p}- j\frac{1}{\omega L_p}} \cdot \frac{\frac{1}{R_p} + j\frac{1}{\omega L_p}}{\frac{1}{R_p} + j\frac{1}{\omega L_p}}\]

Ausmultiplizieren und umstellen:

\[\underline{Z} = -j\frac{1}{\omega C_r} + \frac{\frac{1}{R_p}}{\frac{1}{R_p^2} + \frac{1}{\omega^2 L_p^2}} + j\frac{\frac{1}{\omega L_p}}{\frac{1}{R_p^2} + \frac{1}{\omega^2 L_p^2}} = \frac{\frac{1}{R_p}}{\frac{1}{R_p^2} + \frac{1}{\omega^2 L_p^2}} + j \left( \frac{\frac{1}{\omega L_p}}{\frac{1}{R_p^2} + \frac{1}{\omega^2 L_p^2}} - \frac{1}{\omega C_r} \right)\]

b)

Resonanzbedingung: \(Im\{\underline{Z}\} = 0\)

\[\frac{\frac{1}{\omega L_p}}{\frac{1}{R_p^2} + \frac{1}{\omega^2 L_p^2}} = \frac{1}{\omega C_r}\]

\[\frac{1}{\omega L_p} = \frac{1}{\omega C_r} \cdot \left( \frac{1}{R_p^2} + \frac{1}{\omega^2 L_p^2} \right) = \frac{1}{\omega R_p^2 C_r} + \frac{1}{\omega^3 L_p^2 C_r}\]

\[\frac{1}{L_p} = \frac{1}{R_p^2 C_r} + \frac{1}{\omega^2 L_p^2 C_r}\]

\(\cdot (\omega^2 \cdot C_r \cdot L_p^2)\):

\[\omega^2 L_p C_r = \omega^2 \frac{L_p^2}{R_p^2} + 1\]

eine Seite nach 0 umstellen und \(\cdot (\frac{R_p^2}{\omega^2})\):

\[L_p^2 - R_p^2 C_r \cdot L_p + \frac{R_p^2}{\omega^2} = 0\]

pq-Formel:

\[L_{p1,2} = \frac{R_p^2 C_r}{2} \pm \sqrt{\left( \frac{R_p^2 C_r}{2} \right)^2 - \frac{R_p^2}{(1000 s^{-1})^2}} = \frac{(1\,k\Omega)^2 \cdot 2\,\mu F}{2} \pm \sqrt{\left( \frac{(1\,k\Omega)^2 \cdot 2\,\mu F}{2} \right)^2 - \frac{(1\,k\Omega)^2}{(1000 s^{-1})^2}}\]

\[L_p = 1\,H\]

c)

\[\underline{Z} = -j \frac{1}{\omega C_r} + \frac{R_p \cdot j\omega L_p}{R_p + j\omega L_p} = -j \frac{1}{1000 s^{-1} \cdot 2\,\mu F} + \frac{1\,k\Omega \cdot j \cdot 1000 s^{-1} \cdot 1\,H}{1\,k\Omega + j \cdot 1000 s^{-1} \cdot 1\,H} = 500\,\Omega\]

Aufgabe 11.3 (Anpassung)

(Weißgerber Klausursammlung Abschnitt 3 Aufgabenblatt 1 Aufgabe 3)

[Weißgerber, 2015]

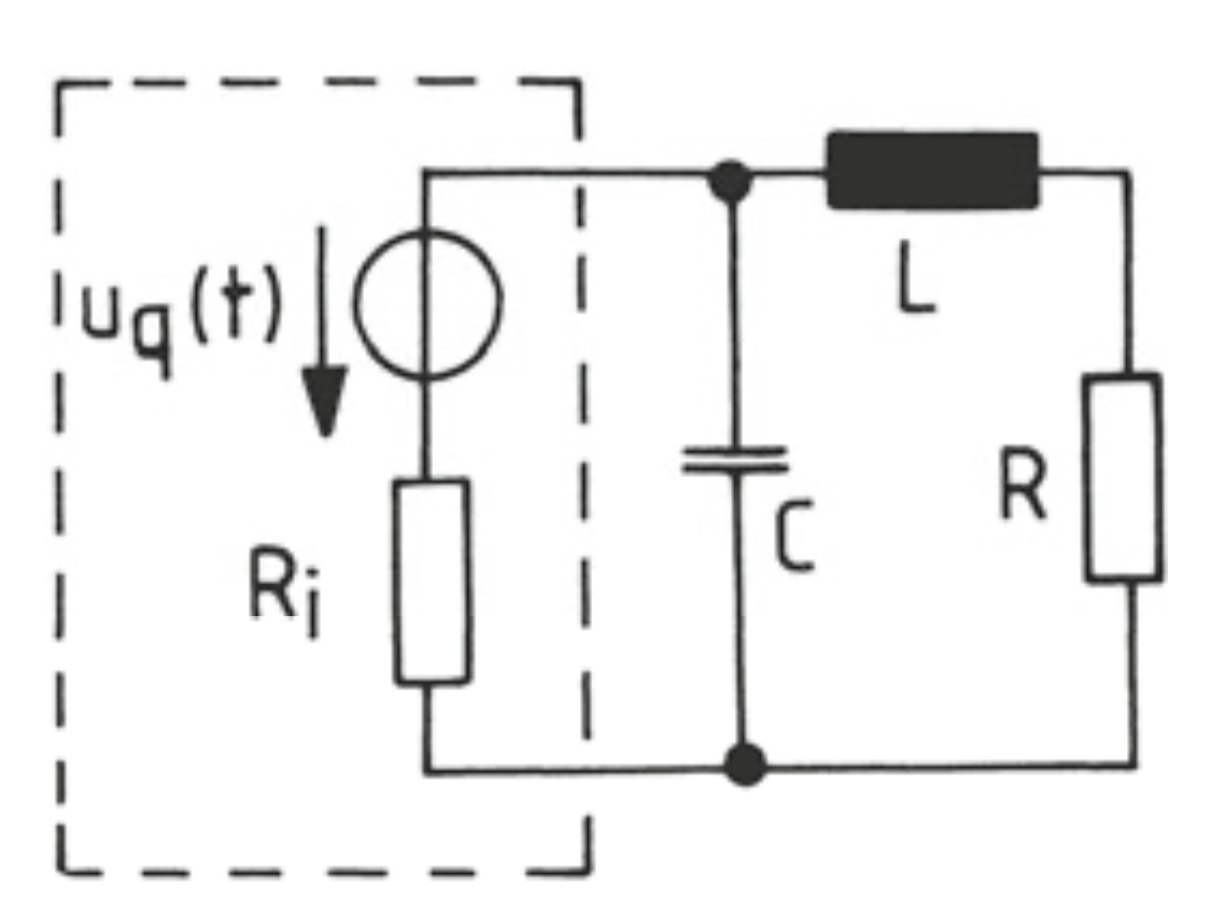
Der Widerstand R soll mit Hilfe der Induktivität L un der Kapazität C an den Widerstand der Energiequelle angepasst werden.

a) Entwicklen Sie zunächst die Bedingung für die Anpassung von aktivem und passivem Zweipol.

b) Berechnen Sie die Werte für L und C für den Fall, dass der Widerstand \(R = 10\,\Omega\) einschließlich der Schaltelemente L und C an die Energiequelle mit dem Innenwiderstand \(R_i = 100\,\Omega\) bei einer Frequenz \(f = 100\,Hz\) angepasst ist.

c) Kontrollieren Sie die Ergebnisse für L und C, indem Sie den Ersatzleitwert \(\underline{Y}_a\) des passiven Zweipols berechnen.

Lösung 11.3

a)

Anpassbedingung:

\[\underline{Z}_a = \underline{Z}_i^*\]

\[\underline{Y}_a = \underline{Y}_i^*\]

Der passive Zweipol ist eine Parallelschaltung, daher bietet sich die Anpassbedingung für Leitwerte an.

\[j\omega C + \frac{1}{R + j\omega L} = \frac{1}{R_i}\]

\[j\omega C + \frac{1}{R + j\omega L} \cdot \frac{R - j\omega L}{R - j\omega L} = \frac{1}{R_i}\]

\[\frac{R}{R^2 + \omega^2 L^2} - j\left( \omega C - \omega \frac{L}{R^2 + \omega^2 L^2}\right) = \frac{1}{R_i}\]

b)

Vergleich Realteil:

\[\frac{R}{R^2 + \omega^2 L^2} = \frac{1}{R_i}\]

\[R \cdot R_i = R^2 + \omega^2 L^2\]

\[L = \frac{\sqrt{R \cdot R_i - R^2}}{\omega} = \frac{\sqrt{10\,\Omega \cdot 100\,\Omega - (10\,\Omega)^2}}{2\pi \cdot 100\,Hz} = 47,74\,mH\]

Vergleich Imaginärteil:

\[j\omega C = j\omega \cdot \frac{L}{R^2 + \omega^2 L^2}\]

\[C = \frac{L}{R^2 + \omega^2 L^2} = \frac{47,74\,mH}{(10\,\Omega)^2 + (2\pi \cdot 100\,Hz)^2 \cdot (47,74\,mH)^2} = 47,74\,\mu F\]

c)

\[\underline{Y}_a = j\omega C + \frac{1}{R + j\omega L} = j\cdot 2\pi \cdot 100\,Hz \cdot 47,74\,\mu F + \frac{1}{10\,\Omega + j \cdot 2\pi \cdot 100\,Hz \cdot 47,74\,mH} = 10\,mS = \frac{1}{R_i} = \frac{1}{100\,\Omega}\]

Bei dem direkten Einsetzten in die Formel bekommt man einen kleinen Imaginärteil (im Bereich \(10^{-6}\)) heraus. In der Originallösung wurde mit Zwischenschritten gearbeitet und gerundet, daher war in der Lösung nur ein reiner Realteil.

Aufgabe 11.4 (Transformator)

(Vaske/Fricke Beispiel 3.117)

[Fricke and Vaske, 1982]

Ein Einphasentransformator für die Nennleistung \(S_N = 500\,kVA\) hat das Leerlauf-Spannungsübersetzungsverhältnis \(\frac{U_1}{U_2} = \frac{20\,kV}{400\,V}\), den relativen Leerlaufstrom \(i_l = 0,015\), die Leerlaufleistungsaufnahme \(P_t = 1\,kW\), die relative Kurzschlussspannung \(u_k = 0,06\) und die Kurzschlussleistungsaufnahme \(P_k = 8\,kW\).

Die auf die Oberspannungsseite bezogenen Widerstände der symmetrischen Ersatzschaltung von dem Bild sind zu bestimmen.

Tipp:

relativer Leerlaufstrom:

\[i_l = \frac{I_l}{I_N}\]

relative Kurzschlussspannung:

\[u_k = \frac{U_k}{U_N}\]

Lösung 11.4

Berechnung des fiktiven Nennscheinwiderstand:

\[Z_{1N} = \frac{U_{1N}}{I_{1N}} = \frac{U_{1N}^2}{S_N} = \frac{(20\,kV)^2}{500\,kVA} = 800\,\Omega\]

Leerlaufversuch:

Wirkfaktor:

\[\cos_{\varphi_l} = \frac{P_l}{i_l \cdot S_N} = \frac{1\,kW}{0,015 \cdot 500\,kVA} = 0,133\]

Scheinwiderstand:

\[Z_{1l} = \frac{U_{1N}}{I_{1l}} = \frac{Z_{1N}}{i_l} = \frac{800\,\Omega}{0,015} = 53,33\,k\Omega\]

die Längswiderstände werden vernachlässigt (Leerlaufversuch):

\[R_{Fe}^{`} = \frac{Z_{1l}}{\cos(\varphi_l)} = \frac{53,33\,k\Omega}{0,133} = 400\,k\Omega\]

\[X_h^{`} = \frac{Z_{1l}}{\sin(\varphi_l)} = \frac{53,33\,k\Omega}{0,9911} = 53,81\,k\Omega\]

Kurzschlussversuch:

Wirkfaktor:

\[\cos(\varphi_k) = \frac{P_k}{u_k \cdot S_N} = \frac{8\,kW}{0,06 \cdot 500\,kVA} = 0,2667\]

Scheinwiderstand:

\[Z_{1k} = \frac{U_{1k}}{I_{1k}} = u_k \cdot Z_{1N} = 0,06 \cdot 800\,\Omega = 48\,\Omega\]

die Querwiderstände werden vernachlässigt (Kurzschlussversuch):

\[R_1 = R_2^{`} = \frac{Z_{1k} \cdot \cos(\varphi_k)}{2} = \frac{48\,\Omega \cdot 0,2667}{2} = 6,4\,\Omega\]

\[X_{1\sigma} = X_{2\sigma}^{`} = \frac{Z_{1k} \cdot \sin(\varphi_k)}{2} = \frac{48\,\Omega \cdot 0,9638}{2} = 23,13\,\Omega\]