2. Komplexe Zahlen

2. Komplexe Zahlen#

imaginäre Einheit
Aufbau komplexer Zahlen
Addition
Subtraktion
Betrag einer komplexen Zahl
Polarkoordinaten
Multiplikation
Division
Kehrwert
Konjugiert-Komplex

Die imaginäre Einheit#

Die imaginäre Einheit j ist definiert als:

\[j^2 = -1\]

Für höhere Potenzen von j erhält man:

\[j^2 = -1\]

\[j^3 = -j\]

\[j^4 = 1\]

\[j^5 = j\]

\[j^6 = -1\]

usw.

Aufbau komplexer Zahlen#

Komplexe Zahlen bestehen aus einem Real- und einem Imaginärteil. Sie werden durch einen Unterstrich gekennzeichnet. Ist der Buchstabe nicht unterstrichen, wird von dem Betrag der Komplexen Zahl geredet.

\[\underline{A} = Re\{\underline{A}\} + j \cdot Im\{\underline{A}\}\]

In der Elektrotechnik wird zur Kennzeichnung des Imaginärteils oft der Buchstabe j anstelle des i verwendet, da das i für die Bezeichnung des Stromes vorhergesehen ist.

Rechenoperationen#

Addition von komplexen Zahlen#

Zwei Komplexe Zahlen $\underline{A}$ und $\underline{B}$ werden addiert, indem ihre Real- und Imaginärteile getrennt voneinander addiert werden.

\[\underline{A} + \underline{B} = Re\{\underline{A}\} + Re\{\underline{B}\} + j(Im\{\underline{A}\} + Im\{\underline{B}\})\]

Subtraktion von komplexen Zahlen#

Zwei Komplexe Zahlen $\underline{A}$ und $\underline{B}$ werden subtrahiert, indem ihre Real- und Imaginärteile getrennt voneinander abgezogen werden.

\[\underline{A} - \underline{B} = Re\{\underline{A}\} - Re\{\underline{B}\} + j(Im\{\underline{A}\} - Im\{\underline{B}\})\]

Betrag einer komplexen Zahl#

Der Betrag einer komplexen Zahl $\underline{A}$ ist die Euklidische Länge des Vektors, wenn dieser zum Beispiel in einem Koordinatensystem gezeichnet ist. Der Betrag wird als $|\underline{A}|$ oder vereinfacht als A geschrieben.

\[A = |\underline{A}| = \sqrt{Re\{\underline{A}\}^2 + Im\{\underline{A}\}^2}\]

Phasenwinkel einer komplexen Zahl#

\[\varphi = arctan\left(\frac{Im\{\underline{A}\}}{Re\{\underline{A}\}}\right)\]

Der Phasenwinkel wird überlicherweise von 0° bis 180° positiv (Zählweise CCW) und von 180° bis 360° negativ (Zählweise CW) angegeben.

Eulersche Identität und Polarkoordinaten#

Komplexe Zahlen können auch als Polarkoordinaten über die Eulersche Identität beschrieben werden. Dabei setzt sich das aus Betrag und Phasenwinkel zusammen.

\[\underline{A} = Re\{\underline{A}\} + j \cdot Im\{\underline{A}\} = A \cdot e^{j\varphi}\]

Eulersche Identität#

\[e^{j\varphi} = cos(\varphi) + j \cdot sin(\varphi)\]

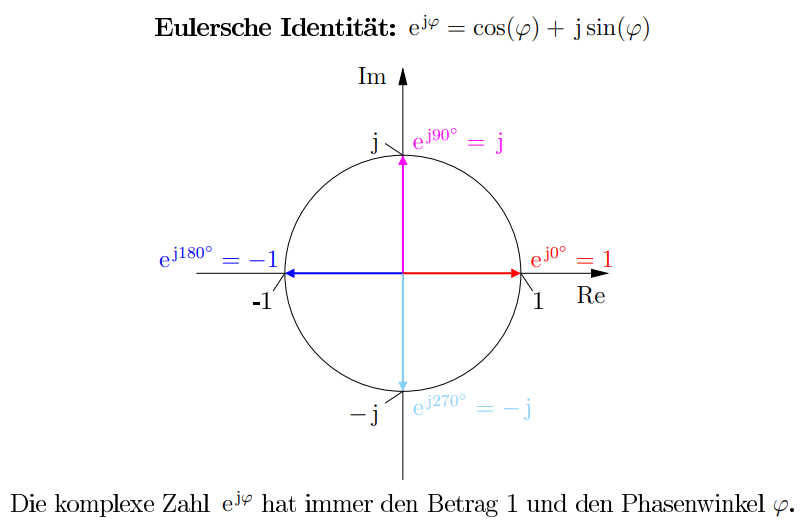
zeigerbild_euler

Die komplexe Zahl $e^{j\varphi}$ hat immer den Betrag 1 und den Phasenwinkel $\varphi$.

Multiplikation komplexer Zahlen#

Die Multiplikation ist über die Polarkoordinaten einfacher.
Bei der Multiplikation werden die Beträge multipliziert und die Phasenwinkel addiert.

\[\underline{A} \cdot \underline{B} = A \cdot B \cdot e^{j(\varphi_A + \varphi_B)}\]

Division komplexer Zahlen#

Ähnlich zur Multiplikation wird bei der Division die Beträge dividiert und die Phasenwinkel subtrahiert.

\[\frac{\underline{A}}{\underline{B}} = \frac{A}{B} \cdot e^{j(\varphi_A - \varphi_B)}\]

Kehrwert einer komplexen Zahl#

Beim Kehrwert einer komplexen Zahl wird der Kehrwert des Betrages genommen und das Vorzeichen des Phasenwinkels invertiert.

\[\frac{1}{\underline{A}} = \frac{1}{A} \cdot e^{-j\varphi}\]

Konjugiert-Komplex#

Bei dem konjugiert-komplexen einer Zahl wird das Vorzeichen des Imaginärteils invertiert. Dadurch verändert sich der Betrag nicht, der Phasenwinkel wird allerdings auch invertiert.

\[\underline{A} = Re\{\underline{A}\} + j \cdot Im\{\underline{A}\}\]

\[\underline{A}^* = Re\{\underline{A}\} - j \cdot Im\{\underline{A}\}\]

Übungen#

Aufgabe 2.1#

$\sqrt{-9} + \sqrt{-x^2} - \sqrt{-y^2} + \sqrt{-25}$

Lösung 2.1

\[3\sqrt{-1} + x\sqrt{-1} - y\sqrt{-1} + 5\sqrt{-1} = j3 + jx - jy + j5 = j(8 +x -y)\]

Aufgabe 2.2#

a) $\frac{3 j^3 \cdot 5 j^4}{6 j^{20}}$

b) $\frac{1}{j^5} + \frac{1}{j^7}$

Lösung 2.2

a) $$\frac{-j3 \cdot 5}{6 i^4} = \frac{-j15}{6} = -j2,5$$

b) $$\frac{1}{j} + \frac{1}{-j} = -j + j = 0$$

Aufgabe 2.3#

a) $(1 + 2j) - (-2 + 3j) + (-3 + j) - (5 + 4j) - (-1 + 9j) + (5 - 8j)$

b) $(-2a + 3j) - (u - uj) + (-2a -3j) - (-u - vj)$

Lösung 2.3

a) 1 - j21

b) -4a + j(u + v)

Aufgabe 2.4#

a) $(5 - 2j)(-3 + j)$ (Ergebnis in kartesischer Form)

b) $\left(3\sqrt{2} + 5\sqrt{3}j\right)\left(3\sqrt{2} - 5\sqrt{3}j\right)$ (Ergebnis in kartesischer Form)

Lösung 2.4

a) -13 + j11

b) 93

Aufgabe 2.5#

a) $\frac{3 + 4j}{2 + j}$

b) $\frac{1}{\sqrt{5} - j}$

c) $\frac{3j}{1 - j}$

Lösung 2.5

a) $\frac{(3 + 4j)(2 - j)}{(2 + j)(2 - j)} = \frac{6 + 8j - 3j + 4}{4 + 1} = 2 + j$

b) $\frac{1(\sqrt{5} + j)}{(\sqrt{5} - j)(\sqrt{5} + j)} = \frac{\sqrt{5} + j}{5 + 1} = \frac{\sqrt{5}}{6} + j\frac{1}{6}$

c) $\frac{3j(1 + j)}{(1 - j)(1 + j)} = \frac{-3 + 3j}{1 + 1}= -\frac{3}{2} + j\frac{3}{2}$

Aufgabe 2.6#

a) $\frac{1 + j}{1 - j} + \frac{1 - j}{1 + j}$

b) $\frac{1 - j}{1 + j} - \frac{1 + j}{1 - j}$

Lösung 2.6

a) $\frac{1 + j}{1 - j} + \frac{1 - j}{1 + j} = \frac{(1 + j)^2 + (1 - j)^2}{(1 - j)(1 + j)} = \frac{1 + 2j - 1 + 1 -2j - 1}{1 + 1} = 0$

b) $\frac{(1 - j)^2 - (1 + j)^2}{(1 + j)(1 - j)} = \frac{1 - 2j - 1 - (1 + 2j - 1)}{1 + 1} = \frac{-4j}{2} = -2j$

Aufgabe 2.7#

In die Exponentialform umwandeln:

a) $0,5 - \sqrt{6}j$

b) $\sqrt{3} + \sqrt{3}j$

c) 3 - 2j

Lösung 2.7

a) $2,5 \cdot e^{j \cdot 4,914}$

b) $2,45 \cdot e^{j \cdot \frac{\pi}{4}}$

c) $3,61 \cdot e^{j \cdot 5,695}$

Aufgabe 2.8#

In die arithmetische Form umwandeln:

a) $83 e^{j \cdot 1,1083}$

b) $3,8 e^{-j \cdot 5,524}$

c) $e^{0,2 + 1,2j}$

Lösung 2.8

a) $83(cos(1,1083) + j sin(1,1083)) = 37,03 + j74,28$

b) $3,8(cos(-5,524) + j sin(-5,524)) = 2,757 + j2,616$

c) $e^{0,2}(cos(1,2) + j sin(1,2)) = 0,443 + j1,138$

Aufgabe 2.9#

Für $z_1 = 1,5 - 0,5j$ und $z_2 = 3 + 0,5j$ die Exponentialform berechnen und die folgende Gleichung in der arithmetischen Form angeben:

\[z = \frac{z_1 \cdot z_2}{z_1 + z_2}\]

Lösung 2.9

\[z_1 = \frac{\sqrt{10}}{2} \cdot e^{-j \cdot 0,322}\]

\[z_2 = \frac{\sqrt{37}}{2} \cdot e^{j \cdot 0,165}\]

\[z_1 + z_2 = 4,5\]

\[\frac{\frac{\sqrt{370}}{4} \cdot e^{j(-0,322 + 0,165)}}{4,5} = 1,069 \cdot e^{-j 0,157} = 1,056 - j0,167\]

Aufgabe 2.10#

Bringe den folgenden Term in die Darstellung $\underline{A} = Re\{\underline{A}\} + j \cdot Im\{\underline{A}\}$:

\[\frac{\frac{1}{j\omega C}}{R + \frac{1}{j\omega C}}\]

Lösung 2.10

\[ \frac{1}{j\omega RC} = \frac{1 - j\omega RC}{(1 + j\omega RC)(1- j\omega RC)} = \frac{1}{1 + (\omega RC)^2} - j\frac{\omega RC}{1 + (\omega RC)^2} \]

Aufgabe 2.11#