Signale

Komplexe Signale

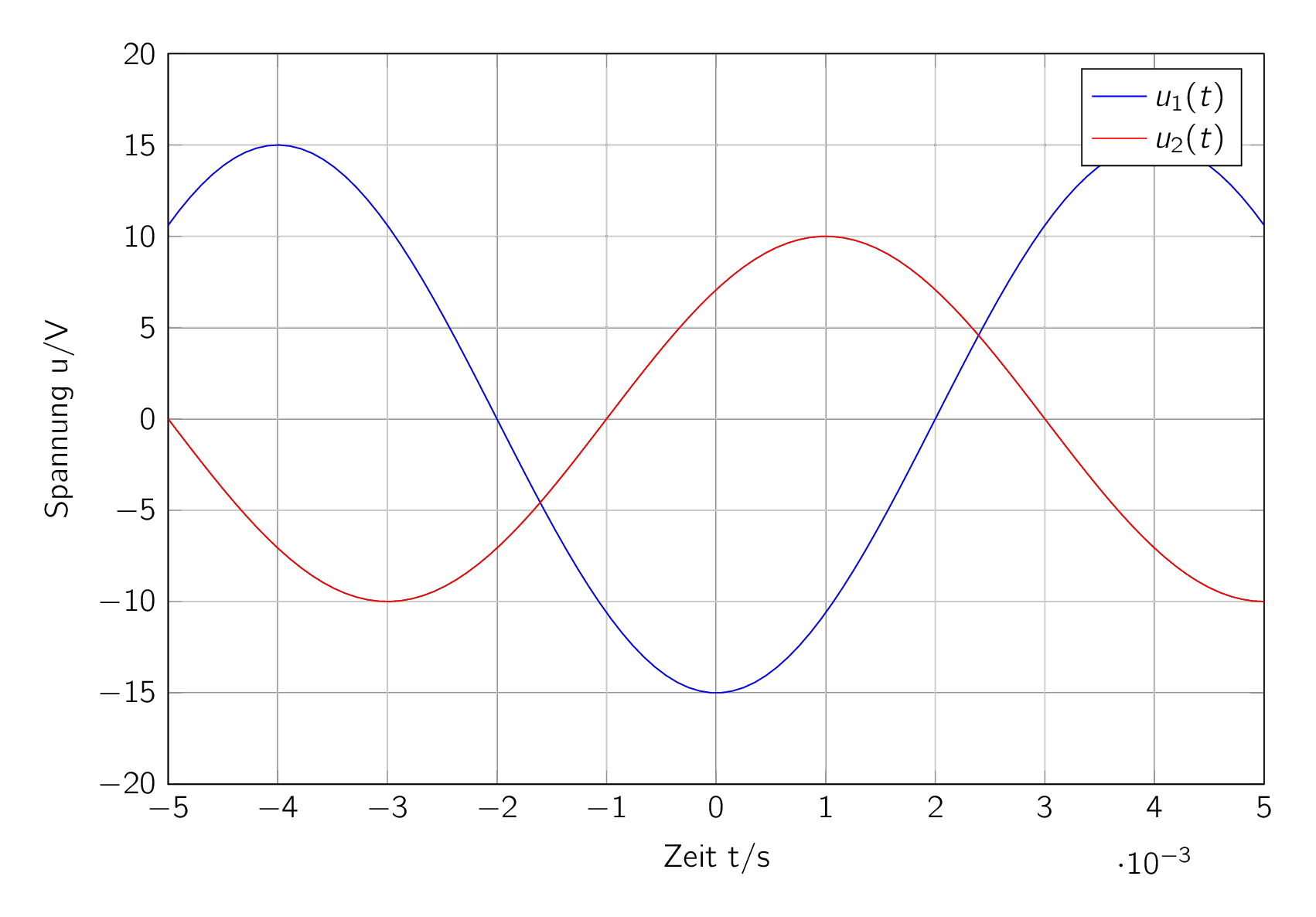
Abb. 25 Oszillogramm der Spannungsmessung.

Mit einem Oszilloskop wird die Zeitabhängigkeit von zwei Sinussignalen, wie in Abb. 25 dargestellt, gemessen.

Signaldarstellung

Geben Sie für die Spannungen \(u_1(t)\) und \(u_2(t)\) folgende Größen an:

• die Periodendauer \(T\)

• die Frequenz \(f\)

• die Kreisfrequenz \(\omega\).

Lösung

\[ T = 8\,ms \]

\[ f = \frac{1}{T}=125\,Hz \]

\[ \omega = 2\pi f = 785\,1/s \]

Sinussignale

Geben Sie für die Darstellungen der Sinus- und Kosinussignale \(u_i(t) = \hat{U}_i \sin(\omega t + \varphi_{ui})\) und \(u_i(t) = \hat{U}_i \cos(\omega t + \psi_{ui})\) die Amplituden \(\hat{U}_i\) und die Phasen \(\varphi_{ui}\) und \(\psi_{ui}\) mit \(i=1,2\) an.

Lösung

Die Amplituden der Spannungen sind \(\hat{U}_1=15\,V\) und \(\hat{U}_2=10\,V\). Die zeitlichen Verläufen können dann wie folgt angegeben werden:

\[ u_1(t) = -\hat{U}_1 \cos(\omega t) = \hat{U}_1 \cos(\omega t \pm \pi) \]

\[ u_1(t) = \hat{U}_1 \sin\left(\omega t - \frac{\pi}{2}\right) \]

\[ u_2(t) = \hat{U}_2 \cos(\omega(t- 1\,ms)) = \hat{U}_2 \cos\left(\omega t - \frac{\pi}{4}\right); \]

\[ u_2(t) = \hat{U}_2 \sin\left(\omega t + \frac{\pi}{4}\right) \]

Übertragungsfaktor

Wenn \(u_1(t)\) die Eingangsspannung und \(u_2(t)\) die Ausgangsspannung einer Schaltung bedeuten, wie groß ist dann der komplexe Übertragungsfaktor \(\underline{H} = \underline{U}_2 / \underline{U}_1\) der Schaltung?

Lösung

Die Umrechnung der reellen Spannungsverläufe in komplexe Größen geschieht über die Funktionaltransformation.

\[\begin{split} u(t) = \operatorname{Re}\left\{\underline{u}(t)\right\} \\ = \operatorname{Re}\left\{\underline{\hat{U}}e^{j\omega t}\right\} \\ = \operatorname{Re}\left\{\hat{U}e^{j(\omega t+\varphi_u)}\right\} \\ =\operatorname{Re}\left\{\hat{U}e^{j\omega t}e^{j\varphi_u}\right\} \\ = \operatorname{Re}\left\{\hat{U}\cos(\omega t + \varphi_u) + j \hat{U} \sin(\omega t + \varphi_u) \right\} \end{split}\]

\[ \underline{u}(t) = \underline{\hat{U}}e^{j\omega t} \quad \mbox{rotierender Zeiger, komplexer Momentanwert} \]

\[ \underline{u}(0) = \underline{\hat{U}}e^{j0}=\hat{U}e^{j\varphi_u} \quad \mbox{ruhender Zeiger, komplexer Scheitelwert} \]

\[ \underline{U} = \frac{1}{\sqrt{2}}\hat{U} e^{j\varphi_u} \quad \mbox{komplexer Effektivwert} \]

\[ \underline{U}_1 = \frac{1}{\sqrt{2}} \hat{U}_1 e^{- j \pi} \]

\[ \underline{U}_2 = \frac{1}{\sqrt{2}} \hat{U}_2 e^{-j\frac{\pi}{4}} \]

\[\begin{split} \underline{H} = \frac{\underline{U}_2}{\underline{U}_1} \\ = \frac{\hat{U}_2 e^{-j\frac{\pi}{4}}}{\hat{U}_1 e^{- j \pi}} \\ = \frac{\hat{U}_2}{\hat{U}_1} e^{j (-\frac{\pi}{4}+\pi)} \\ = \frac{2}{3} e^{j \frac{3}{4}\pi} \end{split}\]

Spannungsverlauf

Zeichnen Sie in das Oszillogramm den Verlauf der Spannung \(u_3(t)\) mit der Frequenz \(f=100\,Hz\) und dem komplexen Scheitelwert \(\underline{\hat{U}}_3 = (15-j 20)\,V\) (karthesische Koordinaten) ein.

Lösung

Darstellung des komplexen Scheitelwertes \(\underline{\hat{U}}_3\) in Polarkoordinaten, Betrag und Phase.

\[ \underline{\hat{U}}_3 = \sqrt{15^2 + 20^2} \exp \left(j \,\arctan\left(\frac{-20}{15}\right)\right) = 25 e^{-j 0.927} \]

\[\begin{split} u_3(t) = \operatorname{Re}\left\{\underline{\hat{U}}_3e^{j\omega_3 t}\right\} \\ = 25\,V \cos(\omega_3 t - 0.927) = 25\,V \cos\left(\omega_3 (t - 1.43\,ms)\right) \end{split}\]

Wirkleistung, Blindleistung und Scheinleistung

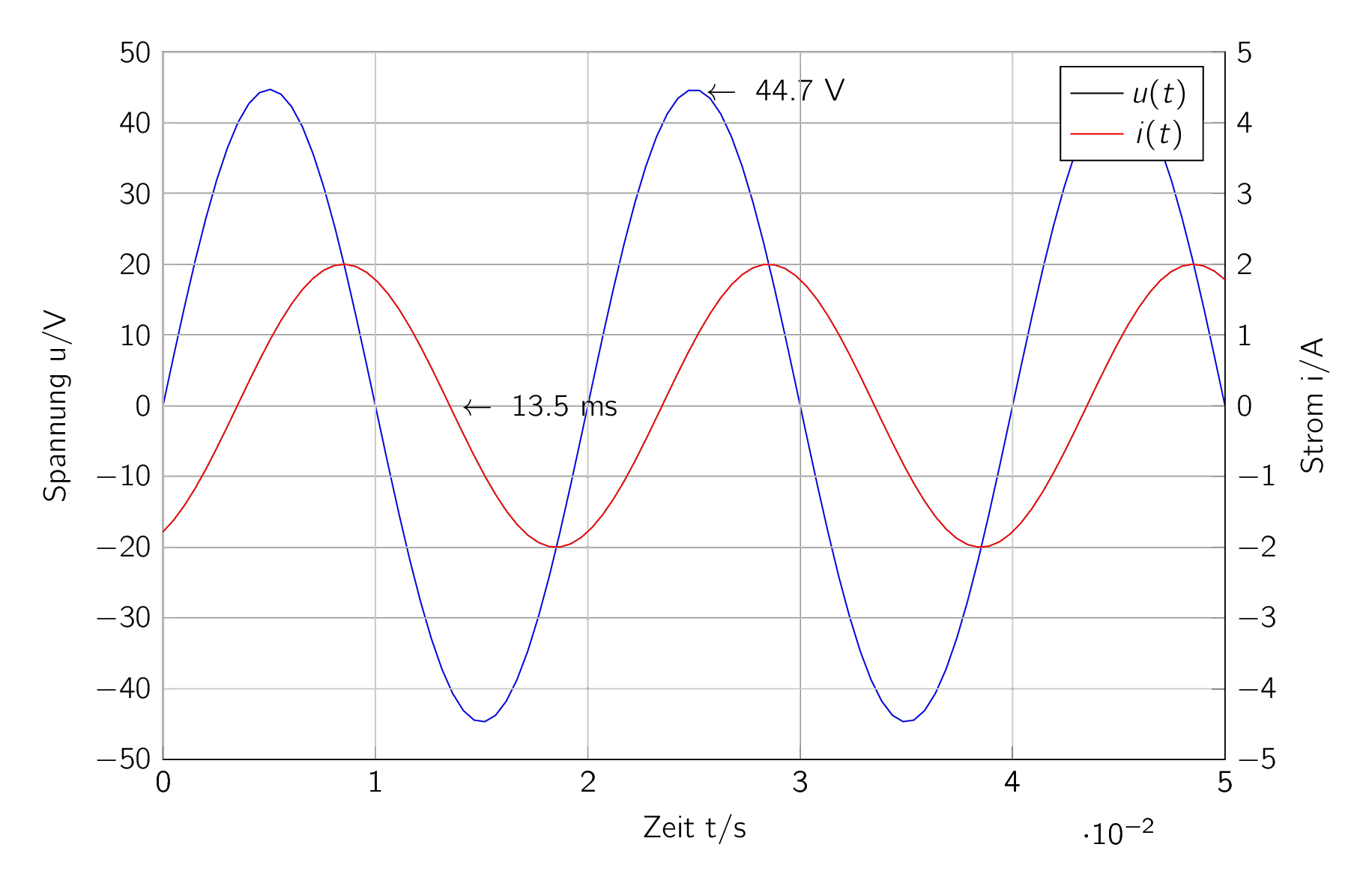
Abb. 26 Oszillogramm der Strom- und Spannungsmessung.

An einem Verbraucher mit der Impedanz \(Z\) wird mittels eines Zweistrahloszilloskops eine zeitaufgelöste Strommessung des Stroms \(i(t)\) durchgeführt. Gleichzeitig wird die Klemmenspannung \(u(t)\) mit aufgenommen. Beide Zeitfunktionen sind sinusförmig. Ihre Amplituden und relativen Lagen sind der Abb. 26 zu entnehmen.

Strom- und Spannungsbeschreibung

Stellen Sie Strom und Spannung in reeller und komplexer Schreibweise dar.

Lösung

1. Reelle Schreibweise

\[ u(t) = \hat{U} \sin(\omega t); \quad \hat{U} = 44.7\,V \]

\[ i(t) = -\hat{I} \sin(\omega (t-\Delta t)); \quad \hat{I}=2\,A, \, \Delta t = 13.5\,ms \]

2. Komplexe Schreibweise

\[ u(t) = \hat{U} \cos\left(\omega t - \frac{\pi}{2} \right) \rightarrow \underline{U} = \frac{1}{\sqrt{2}} \hat{U}e^{-j\frac{\pi}{2}} \]

\[ i(t) = -\hat{I} \cos\left(\omega t- \omega\Delta t -\frac{\pi}{2}\right) \rightarrow \underline{I} = -\frac{1}{\sqrt{2}}\hat{I} e^{-j(\omega \Delta t + \frac{\pi}{2})} \]

Komplexe Leistung

Geben Sie für den Verbraucher die komplexe Leistung \(\underline{P}=P+jQ\) mit aufgenommener Wirkleistung \(P\) und aufgenommener Blindleistung \(Q\) an.

Lösung

\[ \underline{P} = \underline{U} \cdot \underline{I}^* = -\frac{1}{2} \hat{U} \hat{I} e^{-j(\omega \Delta t)} = P + j Q \]

Koeffizientenvergleich:

\[ P = \operatorname{Re}\left\{\underline{P}\right\} = \operatorname{Re}\left\{-\frac{1}{2} \hat{U} \hat{I}e^{-j(\omega \Delta t)}\right\} = -\frac{1}{2} \hat{U} \hat{I}\cos(\omega \Delta t) = 20\,W \]

\[ Q = \operatorname{Im}\left\{\underline{P}\right\} = \operatorname{Im}\left\{-\frac{1}{2} \hat{U} \hat{I}e^{-j(\omega\Delta t)}\right\} = -\frac{1}{2} \hat{U} \hat{I}\sin(\omega \Delta t) = 40\,VA \]

Ersatzschaltung

Geben Sie eine Reihenschaltung und eine Parallelschaltung aus R-, L- und/oder C-Komponenten zur möglichen Realisierung des Verbrauchers an. Bestimmen Sie dazu die Komponentenwerte aus den gemessenen Strom- und Spannungsverläufen.

Lösung

Reihen- oder Parallelschaltung aus Widerstand \(R\) und Induktivität \(L\). Für die Reihenschaltung errechnen sich die Bauteilwerte wie folgt:

\[\begin{split} Z = \frac{\underline{U}}{\underline{I}} \\ = -\frac{\hat{U}}{\hat{I}}e^{j \omega \Delta t} \\ = (10 + j 20)\,\Omega \\ = R_s + j\omega L_s \end{split}\]

\[ R_s = 10\,\Omega \]

\[ L_s = \frac{20}{\omega}\,\Omega=640\,mH \]

Für die Realisierung mit einer Parallelschaltung, Umrechnen der Impedanzwerte in Admittanzwerte.

\[ Y = \frac{1}{R_p}+\frac{1}{j\omega L_p} = \frac{1}{Z} = \frac{1}{R_s+j \omega L_s} = \frac{R_s - j \omega L_s}{R_s^2+(\omega L_s)^2} \]

Ermittlung der Bauteilwerte für die Parallelschaltung durch Koeffizientenvergleich.

\[ \frac{1}{R_p} = \frac{R_s}{R_s^2+(\omega L_s)^2} R_p= 50\,\Omega \]

\[ \frac{1}{\omega L_p} = \frac{\omega L_s}{R_s^2+(\omega L_s)^2} \omega L_p = 25\,\Omega \]

\[ L_p = 796\,mH \]

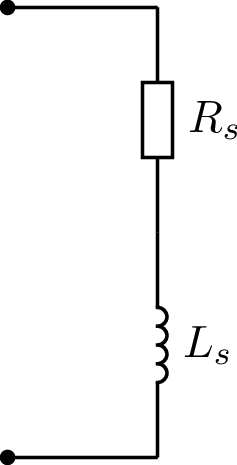
Abb. 27 Ersatzschaltung des Verbrauchers.

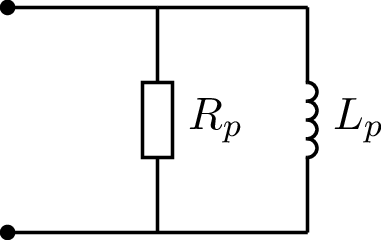
Abb. 28 Ersatzschaltung des Verbrauchers.