Periodische Signale#
Darstellung von Signalen#
Stellen Sie die Signale des angegebenen Netzwerks mit Python (und/oder von Ihnen gewählten alternativen Softwarepaketen des wissenschaflichten Rechnens, z.B. Matlab oder Gnu Octave) dar.
Die Komponenten Werte sind: \(\omega\) = \(2 \pi\) 1 kHz, \(\hat{U}_0\) = 10 V, \(R\) = 30 \(\Omega\), \(L\) = 3 mH, \(\hat{I}_0\) = 0.282 A, \(\varphi_I\) = -32.1 Grad.
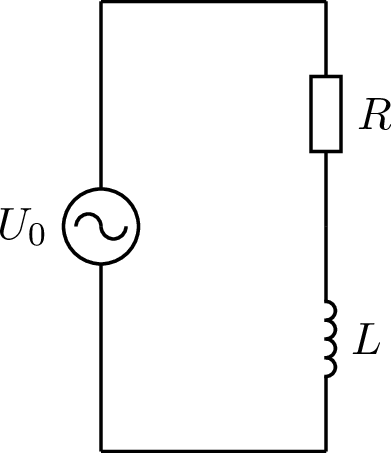
Abb. 21 Wechselstromschaltung.#
Lösung#
import numpy as np
import matplotlib.pyplot as plt
f = 10**3 # Grundfrequenz 1 kHz wird auch als 10e3 geschrieben
w = 2 * np.pi * f # Kreisfrequenz
U0p = 10 # Spannung in Volt
R = 30 # Widerstand in Ohm
L = 3e-3 # Induktivität in Henry
I0p = 0.282 # Strom in Ampere
phiI = -32.1 * np.pi / 180 # Winkel in rad
t = np.linspace(0, 5e-3, 1000) # Zeitachse anlegen
u0 = U0p * np.sin(w * t)
i0 = I0p * np.sin(w * t + phiI)
uL = w * L * I0p * np.sin(w * t + phiI + np.pi / 2) # Spannung über der Spule
uR = R * i0 # Spannung über Widerstand
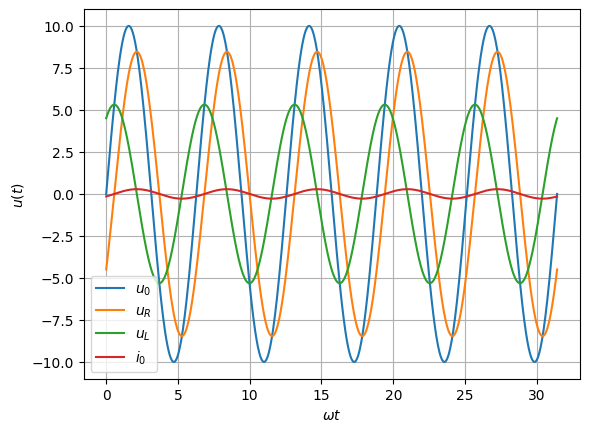
plt.plot(w * t, u0, label=r'$u_0$')
plt.plot(w * t, uR, label=r'$u_R$')
plt.plot(w * t, uL, label=r'$u_L$')
plt.plot(w * t, i0, label=r'$i_0$')
plt.xlabel(r'$\omega t$')
plt.ylabel(r'$u(t)$')
plt.grid()
plt.legend()
plt.show()
Überlagerung von sinusförmigen Spannungen mit verschiedenen Frequenzen#
Der zeitliche Verlauf einer Spannung mit \(\omega_2 = 3 \omega_1\) sei gegeben durch
Periodendauer#
Wie groß ist die Periodendauer \(T\)?
Lösung#
Die Periodendauer \(T\) ist der kleinste Zeitabschnitt mit \(u(t+T)=u(t)\).
Mittelwert#
Berechnen Sie den Mittelwert der Spannung \(u(t)\)!
Lösung#
Effektivwert#
Berechnen Sie den Effektivwert \(U_{eff}\) der Spannung \(u(t)\)! Wie läßt sich \(U_{eff}\) aus den Effektivwerten der drei Einzelspannungen berechnen?
Hinweis
Lösung#
Scheitelfaktor#
Wie groß ist der Scheitelfaktor \(U_{max}/U_{eff}\), wenn \(U_0\) = 1 V, \(\hat{U}_1\) = \(\hat{U}_2\) = 100 mV und \(\varphi\) = 60 Grad?
import numpy as np
import scipy.integrate as si
import scipy.optimize as so
import matplotlib.pylab as plt
U0 = 1
U1p = 100e-3
U2p = 100e-3
phi = 60 * np.pi / 180
f1 = 1e3
T = 1 / f1
w1 = 2 * np.pi * f1
w2 = 3 * w1
# Definition der Spannungen als Funktion
def u(t):
return U0 + U1p * np.cos(w1 * t) + U2p * np.cos(w2 * t + phi)
def u2(t):
return (U0 + U1p * np.cos(w1 * t) + U2p * np.cos(w2 * t + phi))**2
# Zeit als Vektor
t = np.linspace(0, 5e-3, 3000)
# Darstellung der Funktion
fig1 = plt.figure(1)
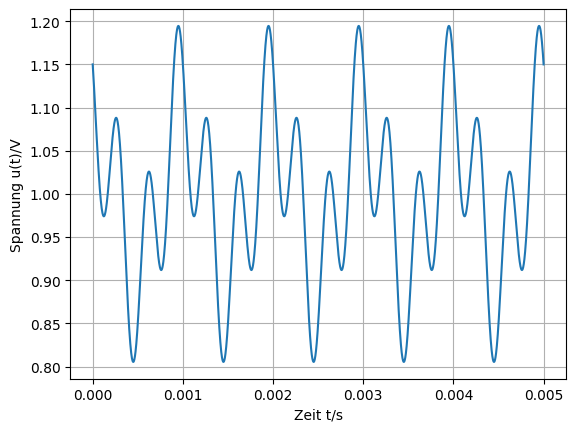
plt.plot(t, u(t))
plt.xlabel('Zeit t/s')
plt.ylabel('Spannung u(t)/V')
plt.grid('on')
plt.show()
# Mittelwert der Spannung u(t)
y, err = si.quad(u, 0, T)
u_bar = 1 / T * y
print('Der Mittelwert:', u_bar)
# Effiktivwert der Spannung u(t)
y2, err2 = si.quad(u2, 0, T)
U_eff = np.sqrt(1 / T * y2)
print('Der Effektivwert:', U_eff)
# Berechnung des Scheitelfaktors, Fixpunkt-Iteration
def func(x, c1, c2, c3):
return 1.0 / 3.0 * (np.arcsin(-c1 / (3 * c2) * np.sin(x)) - c3)
SF = so.fixed_point(func, 1, args=(U1p, U2p, phi), xtol=1e-6)
print('Der Scheitelfaktor:', SF)
Der Mittelwert: 1.0
Der Effektivwert: 1.004987562112089
Der Scheitelfaktor: -0.31462061084367027
Lösung#
Die letzte Gleichung ist eine sog. Fixpunktiteration, deren numerische Lösung im Programmcode formuliert ist. Nach ein paar Iterationschritten erhält man \(\omega_1 t_{max}\) = -0.315. Daraus ergeben sich \(U_{max}\) = 1.195 V und \(U_{eff}\) = 1.005 V.
Der gesuchte Formfaktor berechnet sich zu:
Schaltungsberechnung in reeller Schreibweise#

Abb. 22 Netzwerk zur Schaltungsanalyse.#
Gegeben sei die in Abb. 22 skizzierte Schaltung mit einer Wechselstromquelle \(i_0(t)=\hat{I}_0 \sin(\omega t)\).
Amplitude und Phase#
Berechnen Sie Amplitude und Phasenwinkel jeweils von \(u(t)\), \(i_C(t)\) und \(i_R(t)\)!
Lösung#
Sei \(u(t)=\hat{U} \sin(\omega t + \varphi_u)\), dann ergeben sich die Ströme zu:
Knotengleichung: \(i_0(t) = i_C(t) + i_R(t)\)
Koeffizientenvergleich:
Spannungsverläufe#
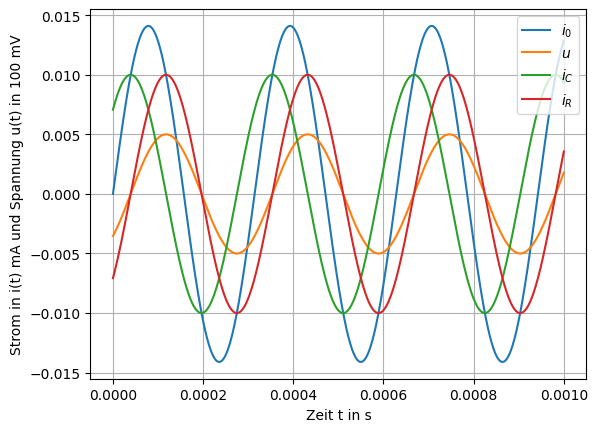
Skizzieren Sie mithilfe von Python \(i_0(t)\), \(u(t)\), \(i_C(t)\) und \(i_R(t)\) für \(\hat{I}_0\) = 14.1 mA, \(f\) = 3.183 kHz, \(R\) = 50 \(\Omega\) und \(C\) = 1 \(\mu\) F!
from numpy import pi, sin, linspace
import matplotlib.pylab as plt
f = 3.183e3 # Frequenz kHz
w = 2 * pi * f # Kreisfrequenz
R = 50 # Widerstand in Ohm
C = 1e-6 # Kapazität in Farad
I0 = 14.1e-3 # Strom
t = linspace(0, 1e-3, 1000) # Länge der x-Achse und
# Strom- und Spannungfunktionen
i_0 = I0 * sin(w * t) # Stromquelle
u = 5e-3 * sin(w * t - pi / 4) # Spannung
i_C = 10e-3 * sin(w * t + pi / 4) # Strom am Kondensator
i_R = 10e-3 * sin(w * t - pi / 4) # Strom am Widerstand
# Plot der Signale
plt.figure()
plt.plot(t, i_0, label='$i_0$')
plt.plot(t, u, label='$u$')
plt.plot(t, i_C, label='$i_C$')
plt.plot(t, i_R, label='$i_R$')
plt.xlabel('Zeit t in s')
plt.ylabel('Strom in i(t) mA und Spannung u(t) in 100 mV')
plt.legend(loc='upper right')
plt.grid()
plt.show()
Lösung#
Mit den Werten ergeben sich folgende Spannungs- und Stromverläufe:
\(i_0(t)\) = 14.1 mA \(\sin(\omega t)\)
\(u(t)\) = 0.5 V \(\sin(\omega t - \frac{\pi}{4})\)
\(i_C(t)\) = 10 mA \(\sin(\omega t + \frac{\pi}{4})\)
\(i_R(t)\) = 10 mA \(\sin(\omega t - \frac{\pi}{4})\)
Phasenanschnittsteuerung#
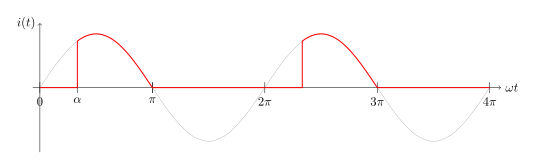
Abb. 23 Halbwelle.#
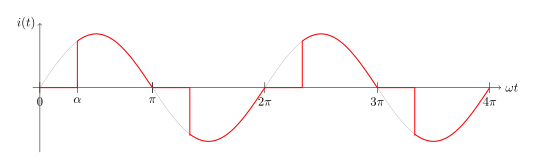
Abb. 24 Vollwelle.#
Das Prinzip der Phasenanschnittsteuerung, bei dem gem. Abb. 23 oder Abb. 24 der Stromfluß in einer Halbwelle auf den zeitlichen Bruchteil \(\pi-\alpha\) begrenzt wird, wird z.B. zum Dimmen von Glühlampen und anderen Kleinverbrauchern im Haushalt verwendet. Der Phasenanschnittwinkel \(\alpha\) kann dabei elektronisch mit Thyristoren im Bereich \(0 \leq \alpha \leq \pi\) eingestellt werden.
In den hier zu untersuchenden Fällen (a) und (b) wird ein ohmscher Verbraucher mit \(R\) = 100 \(\Omega\) mit Netzspannung (\(U_{0,eff}\) = 230 V, \(\omega\) = 2 \(\pi\) 50 Hz) und Phasenanschnittsteuerung betrieben.
Aufgabe#
Berechnen und skizzieren Sie für den durch den Verbraucherwiderstand \(R\) fließenden Strom \(i(t)\) jeweils Mittelwert, Gleichrichtmittelwert und Effektivwert als Funktion vom Phasenanschnittwinkel \(\alpha\)!
Lösung#
Halbwelle
Vollwelle