Netzwerkanalyse

Systemsimulation

Ebene	Maß	Simulation
Atom	0.1 nm
Festkörper/Atomverbund	1.0 nm
Device	0.1 mm	Feld
Transistor/Subkomponenten	1.0 mm
Gatter/Komponenten	10 mm	Verhaltensmodell

Makrotheorie

[Kasper, 2000]

• Mittelwerte charakteristischer Größen des Systems

• Temperatur, Wärmekapazität, Leitfähigkeit etc.

• schwache oder homogene Ortsabhängigkeit

• partielle Differentialgleichungen (PDE’s) der Feldtheorie gehen über in gewöhnliche Differentialgleichungen (ODE’s)

• nur noch dt kein dx (nach dem Ort)

Netzwerksimulation

• Maschenwiderstandsmatrix

• Knotenleitwertmatrix

• mathematisch äquivalente Beschreibungen

• für praktische Berechnungen (Simulation) \(\rightarrow\) Knotenanalyse

Netzwerk

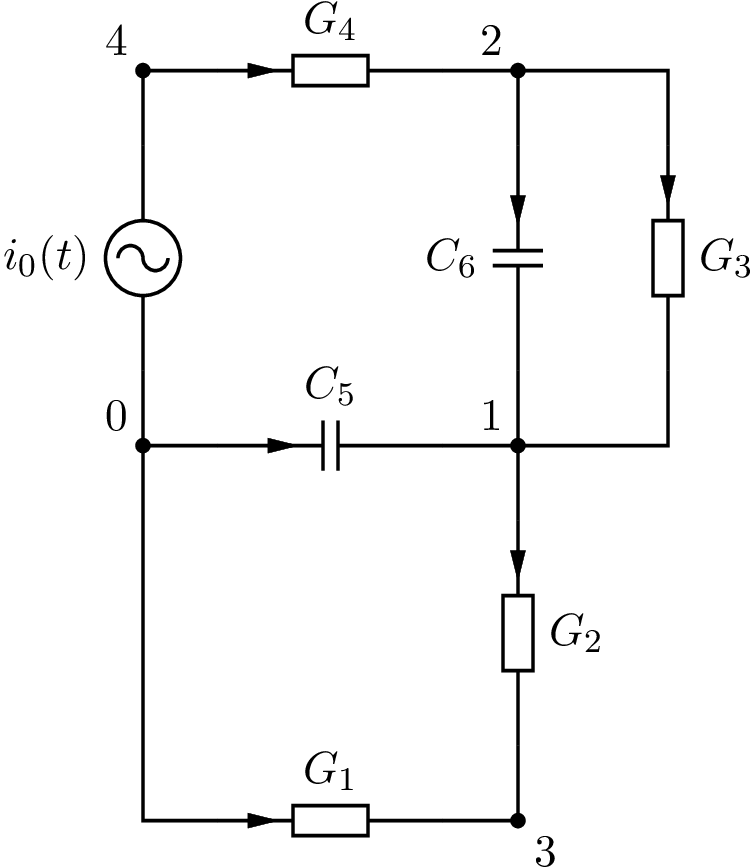
Abb. 5 Netzwerk für die Knotenspannungsanalyse

Transiente Analyse

• Knoten 0:

\[\begin{align*} -i_0-i_1-i_5&=0 \\ -G_1(v_3-v_0) - C_5 \frac{d}{dt}(v_1-v_0) &= i_0 \end{align*}\]

• Knoten 1:

\[\begin{align*} -i_2+i_3+i_5+i_6&=0 \\ -G_2(v_3-v_1)+G_3(v_1-v_3)+C_5 \frac{d}{dt}(v_1-v_0)+C_6 \frac{d}{dt}(v_1-v_6)&=0 \end{align*}\]

• Knoten 2:

\[\begin{align*} -i_3+i_4-i_6 &= 0 \\ -G_3(v_1-v_2)+G_4(v_2-v_4)-C_6 \frac{d}{t}(v_1-v_2) &= 0 \end{align*}\]

Differentialgleichungssystem

\[\begin{align*} \begin{pmatrix} G_2+G_3 & -G_3 & -G_2 & 0 \\ -G_3 & G_3+G_4 & 0 & -G_4 \\ -G_2 & 0 & G_1+G_2 & 0 \\ 0 & -G_4 & 0 & G_4 \end{pmatrix} & \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{pmatrix} + \cdots \\ \begin{pmatrix} C_5+C_6 & -C_6 & 0 & 0 \\ -C_6 & C_6 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \frac{d}{dt} & \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ -i_0 \end{pmatrix} \end{align*}\]

\[\begin{align*} \mathbf{A} \mathbf{x} + \mathbf{B} \dot{\mathbf{x}} &= \mathbf{b} \\ \dot{\mathbf{x}} &= -\mathbf{B}^{-1}\mathbf{A}\mathbf{x} + \mathbf{B}^{-1}\mathbf{b}(t) \\ &= \mathbf{T}\mathbf{x} + \mathbf{g}(t) \end{align*}\]

Netzwerkanalyse zeitabhängiger Signale

• Matrix \(\mathbf{B}\) ist nicht immer invertierbar, ggf. blockweise zerlegen

• Algebro-Differentialgleichungen

• Euler-Verfahren, explizit (vorwärts), implizit (rückwärts)

• Trapez- oder Mittelpunktregel

  • Adams-Bashforth-,Adams-Multon- und Gear-Verfahren

  • Gut für den Rechner \(\rightarrow\) Python, SPICE

  • Wir machen Transformation und dann Gauss’sches-Eliminationsverfahren

Lösung im Frequenzbereich

	Zeitbereich	Frequenzbereich
	Urbildbereich	Bildbereich
Spannung	\(u_n(t)\)	\(\underline{u}(t)=\underline{\hat{U}}e^{j\omega t}\)
Strom	\(i_n(t)\)	\(\underline{i}(t)=\underline{\hat{U}}e^{j\omega t}\)
Widerstand	\(u_R(t)=Ri_R(t)\)	\(\underline{u}_R(t)=R \underline{i}(t)\)
Kondensator	\(i_C(t)=C \frac{du_C(t)}{dt}\)	\(\underline{i}_C(t)= j \omega C \underline{u}_C(t)\)
Spule	\(u_L(t)=L \frac{di_L(t)}{dt}\)	\(\underline{u}_L(t)= j \omega L \underline{i}_L(t)\)
	(wenn für \(t=0\) energielos)

Grundaufgabe der Netzwerkanalyse

• Gewinnung des Netzwerkes

• Wahl des Lösungsverfahrens

• Durchführung der Netzwerkanalyse

• Diskussion der Lösung

Netzwerkgleichungen – Kirchhoff’sche Gesetze

• Knotensatz: \(\sum i_n(t)=0\)

• Maschensatz: \(\sum u_n(t)=0\)

• Zweigbeziehungen: \(u_n = f(i_n)\)

Vollständiges Kirchhoff’sches Gleichungssystem

• \(p=k-1\), unabhängige Knotengleichungen

• \(m=z-(k-1)\), unabhängige Maschengleichungen

• \(z\), \(u,i\)-Beziehungen der Zweigelemente

Netzwerkstruktur

Unabhängige Knoten und Maschen

Die Eigenschaften eines Netzwerkes werden von den Netzwerkelementen und der Netzwerkstruktur oder -topologie bestimmt. Das ist die Art ihrer Zusammenschaltung. Sie wird auch als „Gerüst“ bezeichnet und zeichnerisch durch den „Streckenkomplex“ (engl. graph) ausgedrückt. Die Beschreibung kann gleichwertig durch eine „topologische Matrix“ erfolgen.

Netzwerkgraph

Der Netzwerkgraph beschreibt die Verbindung der Netzwerkelemente durch Abstraktion der Netzwerkgeometrie. Jedem Knoten im Graphen entspricht ein Knoten im Netzwerk und jeder Verbindungslinie ein Zweig zwischen zwei Knoten. Er ist Grundlage der Zahl unabhängiger Knoten- und Maschengleichungen und kann durch „topologische Matrizen“ (sog. „Inzidenzmatrizen“) mathematisch beschrieben werden.

Vollständiger Baum

Ein vollständiger Baum (engl. tree) ist ein Teilgraph, der keine Umläufe besitzt und alle Knoten des Ausgangsgraphen miteinander verbindet. In einem Netzwerk mit \(k\) Knoten hat der vollständige Baum insgesamt \(k-1\) Zweige.

Merkmale

• alle Knoten sind direkt oder indirekt miteinander verbunden,

• wird ein weiterer Zweig entfernt, so geht Merkmal 1. verloren,

• es treten keine Umläufe auf.

Baumkomplement

Das Baumkomplement bildet als Gesamtheit aller Verbindungszweige das „System unabhängiger Zweige“. Jeder Verbindungszweig gehört genau zu einer Schleife (Masche), die nur aus diesem Verbindungszweig und Zweigen des vollständigen Baumes besteht. Eine solche Schleife heißt „Fundamentalschleife“ („unabhängige Masche“). Davon gibt es \(m=z-(k-1)\).

Maschenstromverfahren

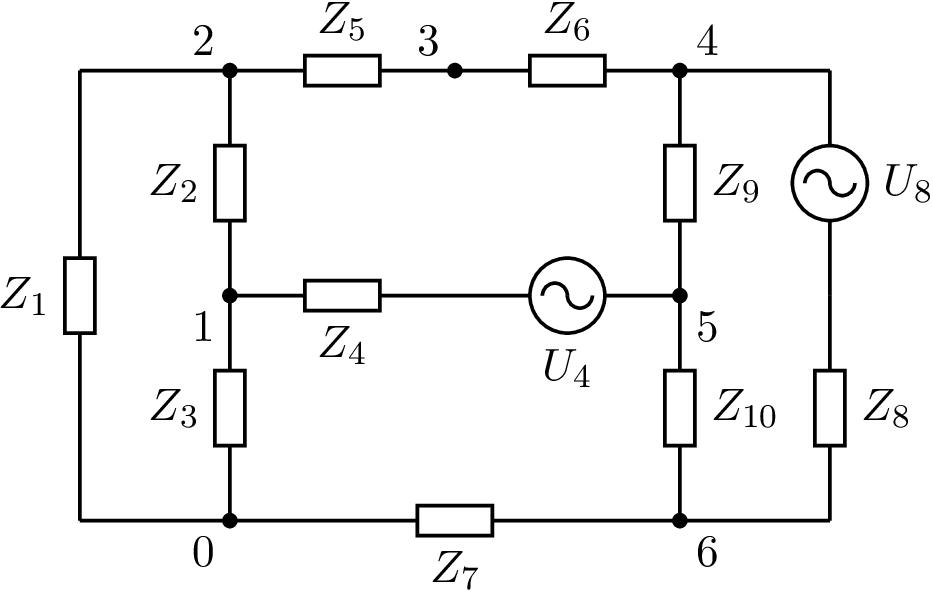
Abb. 6 Netzwerk für die Maschenstromanalyse

Wahl der unabhängigen Ströme \(I_M\)

\[ I_1, I_4, I_7, I_8 \]

Abbildung der abhängigen Ströme durch die unabhängigen Ströme:

(41)\[\begin{align} \begin{pmatrix} I_2 \\ I_3 \\ I_5 \\ I_6 \\ I_9 \\ I_{10} \end{pmatrix} = \begin{pmatrix} -1 & -1 & -1 & 0 \\ -1 & 0 & -1 & 0 \\ 0 & -1 & -1 & 0 \\ 0 & -1 & -1 & 0 \\ 0 & 1 & 1 & -1 \\ 0 & 0 & 1 & -1 \\ \end{pmatrix} \begin{pmatrix} I_1 \\ I_4 \\ I_7 \\ I_8 \end{pmatrix} \end{align}\]

4 Maschengleichungen

(42)\[\begin{align} I_1Z_1 - I_2Z_2 - I_3Z_3 &= 0 \\ U_4 + I_4Z_4 + I_9+Z_9 - I_6Z_6 - I_5Z_5 - I_2Z_2 &= 0 \\ I_7Z_7 + I_{10}Z_{10} + I_9Z_9 - I_6Z_6 - I_5Z_5 - I_2Z_2 - I_3Z_3 &= 0 \\ U_8 + I_8Z_8 - I_9Z_9 - I_{10}Z_{10} &= 0 \end{align}\]

Sortieren und aufstellen des Gleichungssystems:

(43)\[\begin{align} \underbrace{\begin{pmatrix} \sum Z_{1,3} & Z_2 & \sum Z_{2,3} & 0 \\ Z_2 & \sum Z_{2,4,5,6,9} & \sum Z_{2,5,6,9,10} & -Z_9 \\ \sum Z_{2,3} & \sum Z_{2,5,6,9,10} & \sum Z_{2,3,5,6,7,9,10} & \sum -Z_{9,10} \\ 0 & -Z_9 & \sum -Z_{9,10} & \sum Z_{8,9,10} \end{pmatrix}}_{\mathbf{Z}} \underbrace{\begin{pmatrix} I_1 \\ I_4 \\ I_7 \\ I_8 \end{pmatrix}}_{\mathbf{I_M}} &= \underbrace{\begin{pmatrix} 0 \\ -U_4 \\ 0 \\ -U_8 \end{pmatrix}}_{\mathbf{U}} \end{align}\]

Knotenspannungsanalyse

Beim Knotenspannungsverfahren, das auf Maxwell (1873) zurückgeht, wird die Hilfsvariable Knotenspannung so eingeführt, dass jede Maschengleichung automatisch erfüllt ist und daher alle wegfallen.

Das Verfahren umfasst dann:

• die Aufstellung der Knotengleichungen für die Zweigströme,

• ihren Ersatz durch die Zweigbeziehungen \(I=f(U)\) der Netzwerkelemente ausgedrückt durch Knotenspannungen

(statt der Zweigspannung) und die Lösung der Gleichungen nach den Knotenspannungen.

Knotenspannungs- vs Maschenstromanalyse

• Wegfall der Baumsuche, auch spielt die Zahl unabhängiger Maschen \(m = z-(k-1)\) und damit die Anzahl der Zweige keine Rolle,

• weil die Knotenspannungen unabhängige Variablen sind, dürfen Spannungsquellen nicht auftreten, denn eine ideale Spannungsquelle zwischen zwei Knoten macht den Strom durch die Quelle unbestimmt.

Literaturverzeichnis

[Kas00]

Manfred Kasper. Mikrosystementwurf. Springer, Berlin, Germany, 2000.