Audio-Applikationen

Hinweis

Setzen Sie zur Auswertung und graphischen Darstellung der Aufgaben Python und LTspice ein.

Resonanztransformator

Berechnen Sie den Frequenzgang der komplexen Amplitude \(\underline{H}_u(f)=U_1(f)/U_0(f)\) der folgenden Transformator-Schaltung eines dynamischen Mikrofons Abb. 47.

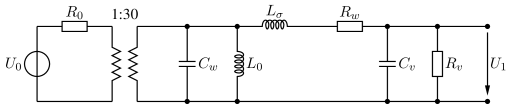
Abb. 47 Ersatzschaltung eines dynamischen Mikrofons.

(85)\[\begin{align} R_0 &= 3\,\Omega, \, \text{Innenwiderstand des Mikrofons} \\ L_0 &= 25\,H, \, \text{Hauptinduktivität} \\ L_{\sigma} &= 1\,H, \, \text{Streuinduktivität} \\ R_w &= 100\,\Omega, \, \text{Wicklungswiderstand} \\ C_w &= 800\,pF, \, \text{Wicklungskapazität} \\ R_u &= 100\,k\Omega, \, \text{Verstärker-Eingangswiderstand} \\ C_u &= 200\,pF, \, \text{Verstärker- und Kabelkapazität} \\ \end{align}\]

Stellen Sie die Ergebnisse als Funktion der Frequenz grafisch dar:

1. als Ortskurve in der komplexen Ebene,

2. als Betrag \(\lvert \underline{H}_u \lvert\) und Phase \(\phi_{H_u}\) über \(\log(f/f_0)\) (normierte Frequenz) und

3. als Bode-Darstellung \(20 \cdot \log \lvert \underline{H}_u \lvert\) über \(\log(f/f_0)\) (normierte Frequenz).

Bei der Analyse und Erläuterung interessieren Grenzfrequenzen, Eckfrequenzen, Hochpass/Tiefpass-Verhalten, die Resonanz-Güte und die Rolle der einzelnen Komponenten im Hinblick auf die genannten Frequenzen.

Lösung

Um den idealen Tranformator aufzulösen muss man:

1. \(R_0\) auf die Sekundärseite transformieren; erscheint dort als \(R_{0s}=R_0/\text{ü}^2\) mit ü=1/30.

2. \(U_0\) durch eine sekundärseitige Ersatzspannungsquelle \(U_{0s}=U_0/\text{ü}\) ersetzen.

Neues Netzwerk:

(86)\[\begin{align} U_1 &= \frac{Z_v}{Z_v + Z_2} U_h & U_h &= \frac{Z_1 || (Z_2+Z_v)}{R_{0s} + (Z_1 || (Z_2 + Z_v))} U_{0s} \end{align}\]

(87)\[\begin{align} H = \frac{U_1}{U_0} = \frac{U_1}{\text{ü} U_{0s}} &= \frac{1}{\text{ü}} \frac{Z_v}{Z_v + Z_2} \frac{Z_p}{R_{0s} + Z_p} \end{align}\]

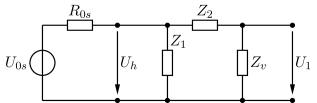
mit

(88)\[\begin{align} Y_1 = \frac{1}{Z_1} &= j \omega C_w + \frac{1}{j \omega L_0}; & Z_2 &= R_w + j \omega L_{\sigma} \\ Y_v = \frac{1}{Z_v} &= j \omega C_v + \frac{1}{R_v}; & Z_p &= Z_1 || (Z_2+Z_v) = \frac{Z_1(Z_2+Z_v)}{Z_1+Z_2+Z_v} \end{align}\]

import numpy as np
import matplotlib.pyplot as plt


# %% Spezifikation
R0 = 3  # Innenwiderstand des Mikrofons
L0 = 25  # Hauptinduktivitaet
Ls = 1  # Streuinduktivitaet
Rw = 100  # Wicklungswiderstand
Cw = 800e-12  # Wicklungskapazitaet
Rv = 100e3  # Verstaerker-Eingangswiderstand
Cv = 200e-12  # Verstaerker- und Kabelkapazitaet
u = 1/30  # Uebertragungsfaktor u1/u2

# %% Frequenzvektor
f = np.logspace(0, 5, 1000)
w = 2 * np.pi * f
f0 = 1

# %% Impedanzen/Admittanzen
Y1 = 1j*w*Cw + 1/(1j*w*L0)
Z1 = 1/Y1

Yv = 1j*w*Cv + 1/Rv
Zv = 1/Yv

Z2 = Rw + 1j*w*Ls

Zp = Z1*(Z2 + Zv)/(Z1 + Z2 + Zv)

R0q = R0/u**2

# %% Uebertragungsfunktion
H = 1/u * Zv/(Z2 + Zv) * Zp/(R0q + Zp)


# %% Ortskurve von H(f)
fig1 = plt.figure(1)
plt.title('H-Ebene')
plt.plot(np.real(H), np.imag(H))
plt.xlabel('Re')
plt.ylabel('Im')
plt.legend(('H'))
plt.grid()
plt.show()


# %% Betrag und Phase von H(f)
fig2 = plt.figure(2)
plt.title('Betrag und Phase')
plt.subplot(211)
plt.semilogx(f, np.abs(H))
# plt.xlabel(r'$\log(f/f_0)$')
plt.ylabel(r'|H|')
plt.grid()
plt.subplot(212)
plt.semilogx(f, np.angle(H))
plt.xlabel(r'$\log(f/f_0)$')
plt.ylabel(r'arg(H)')
plt.grid()
plt.show()


# %% Betragsfrequenzgang von H(f)
H_dB = 20*np.log10(np.abs(H))

fig3 = plt.figure(3)
plt.title('Betragsfrequenzgang')
plt.semilogx(f, H_dB)
plt.xlabel(r'$\log(f/f_0)$')
plt.ylabel(r'$|H|$ in dB')
plt.grid()
plt.show()

Ersatzschaltbild eines Lautsprechers

Die dargestellte Schaltung in Abb. 48 ist ein vereinfachtes Ersatzschaltbild eines elektrodynamischen Lautsprechers. Dabei repräsentiert \(\underline{Z}_1 = R_1 + j \omega L_1\) die Impedanz der ruhenden Schwingspule und \(\underline{Z}_M\), die Parallelschaltung aus \(R_2\), \(L_2\) und \(C_2\), repräsentiert die dynamisch-mechanischen Eigenschaften des Systems.

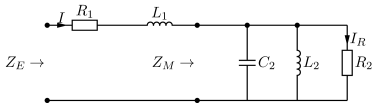
Abb. 48 Ersatzschaltbild eines Lautsprechers.

\[ R_1 = 3\,\Omega, L_1 = 200\,\mu H, C_2 = 1000\,\mu F, L_2 = 4\,mH, R_2 = 30\,\Omega \]

Eingangsimpedanz

Drücken Sie die Eingangsimpedanz \(\underline{Z}_E\) der Schaltung als Funktion der verwandten Bauteile (\(R_1\), \(L_1\), \(R_2\), \(L_2\), \(C_2\)) und der Kreisfrequenz \(\omega\) aus.

Lösung

(89)\[\begin{align} Y_M &= \frac{1}{Z_M} = j \omega C_2 + \frac{1}{j \omega L_2} + \frac{1}{R_2} \\ &= \frac{1 - \omega^2 L_2 C_2 + j\frac{\omega L}{R_2}}{j \omega L_2} \\ Z_E &= R_1 + j \omega L_1 + Z_M \\ &= R_1 + j \omega L_1 + \frac{j \omega L_2}{1 - \omega^2 L_2 C_2 + j\frac{\omega L}{R_2}} \end{align}\]

Ortskurve

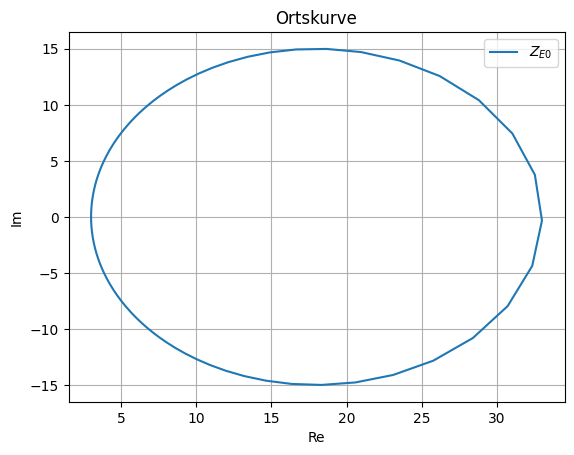
Für niedrige Frequenzen (\(0 \leq f \leq 100\,Hz\)) kann der Beitrag \(\omega L_1\) der Induktivität \(L_1\) zur Eingangsimpedanz vernachlässigt werden. Konstruieren Sie mit dieser Vereinfachung die Ortskurve der Eingangsimpedanz \(\underline{Z}_{E0}\) als Funktion der Kreisfrequenz \(\omega\).

Lösung

\[ Z_{E0} = R_1 + Z_M \]

Konstruktion der Ortskurve \(Z_{E0}(\omega)\):

• \(Y_M\) zeichnen: Gerade

• \(Y_M\) invertieren \(\rightarrow Z_M\): Kreis

• \(R_1\) addieren \(\rightarrow Z_{E0}\): verschobener Kreis

Wert der Impedanz

Berechnen Sie den Wert der Impedanz \(\underline{Z}_{E0}\) bei der Frequenz \(f\) = 100 Hz.

Lösung

\[ Z_{E0}(f=100\,Hz) = (3,6 - j 4,25) \Omega \]

Ortskurve

Geben Sie näherungsweise die Ortskurve der Impedanz \(\underline{Z}_E\) als Funktion der Kreisfrequenz \(\omega\) an, inklusive des Beitrags der Induktivität \(L_1\).

Lösung

Für \(f \leq 100\,Hz\) ist \(\omega L_1 \leq 0.125\), daraus folgt für \(f \leq 100\,Hz\) dass \(Z_E \approx Z_{E0}\). Für \(f >> 100\,Hz\) ist \(Z_{E0} \approx R_1\) und \(Z_E \approx R_1 + j \omega L_1\).

Bode-Diagramm

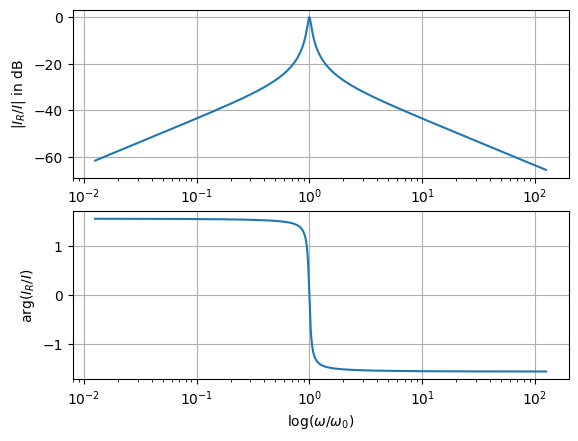
Der Lautsprecher werde aus einer Sinusspannungsquelle mit \(\hat{U}_0\) = 10 V und Innenwiderstand \(R_i\) = 0,5 \(\Omega\) gespeist. Stellen Sie das Verhältnis der Effektivwerte von \(I_R\) und \(I\) sowie den Phasenwinkel von \(I_R\) zu \(I\) als Funktion der Frequenz in einem Bode-Diagramm dar.

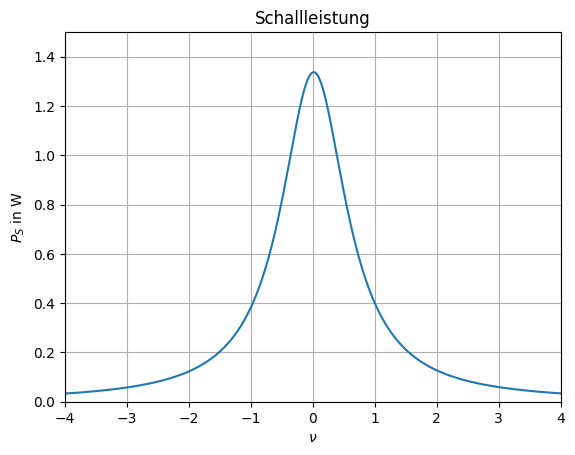
Berechnen Sie die abgestrahlte Schallleistung \(P_S = R I^2_{R,eff}\) als Funktion der normierten Verstimmung \(\nu = \omega/\omega_0 - \omega_0/\omega\), wobei \(\omega_0=(L_2 C_2)^{-1/2}\) ist, und stellen Sie \(P_S(\nu)\) graphisch dar. Wie groß ist die von der Schaltung aufgenommene Wirkleistung bei \(\omega=\omega_0\)?

Lösung

(90)\[\begin{align} \frac{I_R}{I} &= \frac{Z_M}{R_2} = \frac{j \omega L_2}{R_2(1 - \omega^2 L_2C_2) + j \omega L_2} \\ &= \frac{1}{1 + R_2 \left(\frac{1}{ j\omega L_2} + j \omega C_2 \right)} \\ &= \frac{1}{1 + j R_2 \sqrt{\frac{C_2}{L_2}}\left(\omega \sqrt{L_2C_2} - \frac{1}{\omega\sqrt{L_2C_2}}\right)} \\ &= \frac{1}{1 + j Q \underbrace{\left(\frac{\omega}{\omega_0} - \frac{\omega_0}{\omega}\right)}_{\nu}} \end{align}\]

Die Güte \(Q=\frac{R_2}{\sqrt{\frac{L_2}{C_2}}}=15\).

\[ \frac{I_{R,eff}}{I_{eff}} = \frac{\lvert I_R \lvert}{\lvert I \lvert} = \frac{1}{\sqrt{1 + Q^2 \nu^2}} \]

Eine vernünftige Darstellung ist doppelt-logarithmisch (Bode-Diagramm).

\[ \varphi = \arg\left(\frac{I_r}{I}\right) = -\arctan \left(Q \nu \right) \]

Die Schallleistung ergibt sich wie folgt:

(91)\[\begin{align} P_S &= R_2 I^2_{R,eff} = R_2 I^2_{eff} \frac{I^2_{R,eff}}{I^2_{eff}} \\ &= R_2 \frac{\frac{\hat{U}^2_0}{2}}{\lvert Z_E + R_i \lvert^2} \frac{1}{1 + Q^2 \nu^2} \end{align}\]

Für die exakte Berechnung \(Z_E\) aus the section ex:ZE einsetzen, genähert the section ex:ZE0 benutzen. Wenn \(\omega = \omega_0\), dann \(\nu = 0\):

\[ P_S \approx R_2 \frac{\frac{\hat{U}^2_0}{2}}{\left( R_1 + R_i + R_2 \right)^2} = 1,3\,W \]

import numpy as np
import matplotlib.pyplot as plt


# %% Spezifikation
L1 = 200e-6
R1 = 3
C2 = 1000e-6
L2 = 4e-3
R2 = 30

# %% Frequenzvektor
f = np.logspace(0, 4, 2000)
w = 2 * np.pi * f

# %% Impedanzen/Admittanzen
YM = 1j*w*C2 + 1/(1j*w*L2) + 1/R2
ZM = 1/YM

ZE = R1 + 1j*w*L1 + ZM

ZE0 = R1 + ZM


# %% Ortskurve von ZE0(w)
fig1 = plt.figure(1)
plt.title('Ortskurve')
plt.plot(np.real(ZE0), np.imag(ZE0), label=r'$Z_{E0}$')
plt.xlabel('Re')
plt.ylabel('Im')
plt.legend()
plt.grid()
plt.show()


# %% Uebertragungsfunktion
Q = R2/(np.sqrt(L2/C2))  # Guete
print(Q)

w0 = 1/np.sqrt(L2*C2)
print(w0)

v = (w/w0 - w0/w)  # Verstimmung

HI = 1/(1 + 1j*Q*v)
HI_dB = 20*np.log10(np.abs(HI))
w_w0 = w/w0

# %% Betrag und Phase von HI(w/w0)
fig2 = plt.figure(2)
plt.title('Betrag und Phase')
plt.subplot(211)
plt.semilogx(w_w0, HI_dB)
plt.ylabel(r'$|I_R/I|$ in dB' )
plt.grid()
plt.subplot(212)
plt.semilogx(w_w0, np.angle(HI))
plt.xlabel(r'$\log(\omega/\omega_0)$')
plt.ylabel(r'$\arg(I_R/I)$')
plt.grid()
plt.show()


# %% Schallleistung Ps
U0s = 10
Ri = 0.5

Ps = R2 * (U0s**2/2)/(np.abs(ZE + Ri)**2) * 1/(1 + Q**2 * v**2)

fig3 = plt.figure(3)
plt.title(r'Schallleistung')
plt.plot(v, Ps)
plt.xlabel(r'$\nu$')
plt.ylabel(r'$P_S$ in W')
plt.axis([-4, 4, 0, 1.5])
plt.grid()
plt.show()

15.0
500.0

/var/folders/bs/dl5x4l2n6xv6ywrg8knjtw440000gn/T/ipykernel_23939/2282262599.py:52: MatplotlibDeprecationWarning: Auto-removal of overlapping axes is deprecated since 3.6 and will be removed two minor releases later; explicitly call ax.remove() as needed.
  plt.subplot(211)