Spannungsteiler

Schaltungsaufgabe mit Zeigerdiagramm

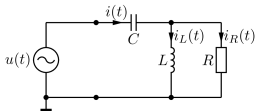
Abb. 29 RLC-Schaltung für das Zeigerdiagramm.

Gegeben ist die RLC-Schaltung in Abb. 29. Dabei sind die Bauteilwerte \(R=100\,\Omega\), \(L=1\,\mu H\), \(C=1\,nF\) und die Spannungsquelle \(u(t)=\hat{U} \cos(\omega t)\) mit \(\hat{U}=1,41\,V\) und \(\omega=2 \pi 6\,MHz\).

Zeigerdiagramm

Die Aufgabe besteht darin, das Zeigerdiagramm für alle Teilströme und Teilspannungen zu erstellen

Schrittweise graphische Lösung

1. \(\vec{I_R}\) und \(\vec{U_R}\) sind reelle Zeiger in Phase. Diese beiden Zeiger als Bezug mit selbst definierten Längen einzeichnen, z.B. \(\vec{I_R} = 5\,cm\) und \(\vec{U_R} = 10\,cm\).

2. \(\vec{I_L}\) mit -90\(^{\circ}\) bezüglich \(\vec{U_R}\) einzeichnen. Zur Bestimmung der Länge muss nun der Zeiger für den Strom durch die Induktivität im Bezug zum Zeiger für den Strom durch den Widerstand bestimmt werden, da Strom- und Spannungszeiger am Widerstand als Referenz für das Zeigerdiagramm zu Beginn gesetzt worden sind.

\[ \vert\vec{I_L}\vert = \frac{\vert\vec{U_L}\vert}{\omega L} = \frac{\vert\vec{U_R}\vert}{\omega L} = \frac{\vert\vec{U_L}\vert}{R}\frac{R}{\omega L} = \vert\vec{I_R}\vert \cdot 2.65 \]

3. Jetzt den Summenvektor für den Gesamtstrom \(\vec{I}=\vec{I_R}+\vec{I_L}\) einzeichnen.

4. Die Spannung am Kondensator mit -90\(^{\circ}\) bezüglich \(\vec{I}\) einzeichnen. Wie auch schon beim Strom durch die Induktivität wird die Länge des Zeigers für die Spannung am Kondensator durch einen Faktor zum Referenzzeiger, \(\vec{U_R}\), ausgedrückt.

\[ \vert\vec{U_C}\vert = \frac{\vert\vec{I}\vert}{\omega C} = \frac{\vert\vec{I}\vert}{\vert\vec{I_R}\vert} \cdot \frac{\vert\vec{I_R}\vert}{\omega C} = \frac{\vert\vec{I}\vert}{\vert\vec{I_R}\vert} \cdot R \vert\vec{I_R}\vert \cdot \frac{1}{\omega R C} = 2.85 \cdot \vert\vec{U_R}\vert \cdot 0.265 = 0.76 \vert\vec{U_R}\vert \]

5. Final den Summenvektor für die Quellenspannung einzeichnen; \(\vec{U} = \vec{U_C} + \vec{U_R}\)

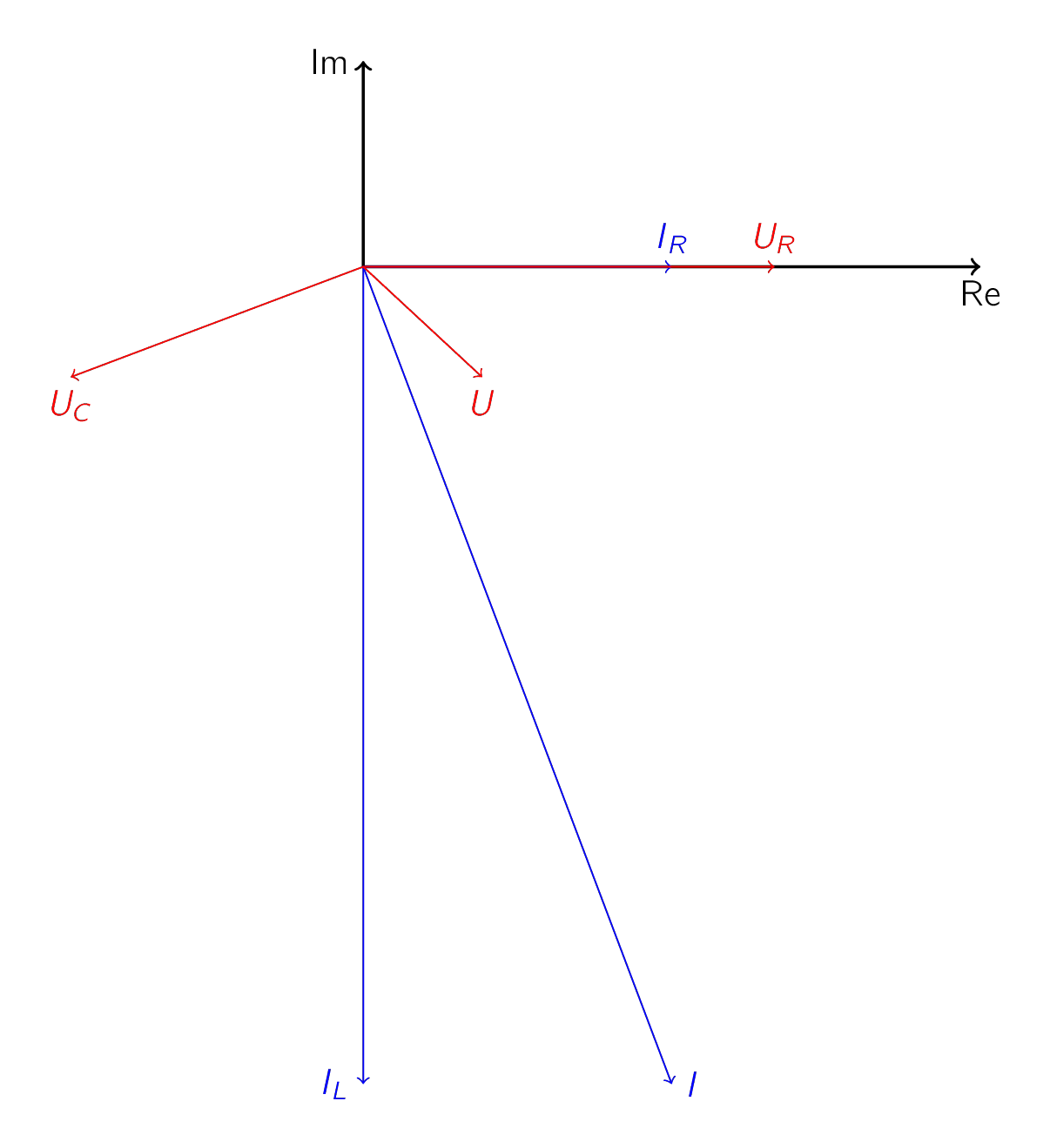
Abb. 30 Zeigerdiagramm.

Kompensierter Spannungsteiler

Die abgebildete Schaltung in Abb. 31 stellt das Prinzip eines Oszilloskoptastkopfes dar, ein sogenannter kompensierter Spannungsteiler. Dabei bezeichnen \(R\) und \(C\) Widerstand und Kapazität des Oszilloskopeingangs. \(R_1 = 9\,M\Omega\), \(R = 1\,M\Omega\), \(R_2 = 1\,M\Omega\), \(C = 10\,pF\).

Abb. 31 Ersatzschaltbild eines Oszilloskop-Tastkopfes.

vgl. Kapazitiver Spannungsteiler [Mietke, 2024]

Spannungsteiler

Leiten Sie den Spannungsübertagungsfaktor \(\underline{H}_u=\underline{U}_{osz}/\underline{U}\) allgemein für die angegebenen Bauteile her?

Lösung

Zeichnen Sie ein vereinfachtes Ersatzschaltbild mit zusammengefassten Impedanzen \(Z_1\) und \(Z_2\).

Abb. 32 Ersatzschaltbild des Tastkopfes zusammengefasst.

(63)\[\begin{equation} Z_1 = \frac{\frac{R_1}{j\omega C_1}}{\frac{1}{j \omega C_1} + R_1} = \frac{R_1}{1 + j \omega R_1 C_1} \end{equation}\]

(64)\[\begin{equation} Z_2 = \frac{R_{2g}}{1+ j \omega R_{2g} C}, \quad \mbox{wobei} \quad R_{2g}=\frac{R_2 R}{R_2+R} \end{equation}\]

Mit diesen Definitionen bestimmt man das Spannungsverhältnis:

(65)\[\begin{equation} \underline{H}_u = \frac{\underline{U_{osz}}}{\underline{U}}= \frac{\underline{Z}_2}{\underline{Z}_1 + \underline{Z}_2}. \end{equation}\]

Eingangsimpedanz

Wie groß ist die Eingangsimpedanz \(\underline{Z}=\underline{U}/\underline{I}\) des Tastkopfes?

Lösung

Mit den Vorarbeiten aus Spannungsteiler kann man an dieser Stelle die Eingangsimpedanz des Tastkopfes als Reihenschaltung der Impedanzen \(Z_1\) und \(Z_2\) notieren.

(66)\[\begin{equation} \underline{Z} = \underline{Z}_1 + \underline{Z}_2 = \frac{R_1}{1 + j \omega R_1 C_1} + \frac{R_{2g}}{1+ j \omega R_{2g} C} \end{equation}\]

Kapazität

Wie muß die Kapazität \(C_1\) gewählt werden, damit das Verhältnis \(\underline{H}=\underline{U}_{osz}/\underline{U}\) für alle Frequenzen gleich groß ist?

Lösung

Ähnlich einer Abgleichbedingung für eine Wechselstrommessbrücke kann man an dieser Stelle argumentieren, dass das Spannungsverhältnis \(\underline{H}\) für alle Frequenzen gleich groß ist, sofern \(R_1C_1 = R_{2g}C\) gilt.

Die mathematische/ingenieurische Begründung ist wie folgt:

(67)\[\begin{equation} \frac{1}{Z_1} = \frac{1}{R_1} + j \omega C_1 \end{equation}\]

(68)\[\begin{equation} \frac{1}{Z_2} = \frac{1}{R_{2g}} + j \omega C \end{equation}\]

(69)\[\begin{equation} \underline{H} = \frac{U_{osz}}{U} = \frac{Z_2}{Z_1 + Z_2} = \frac{1}{1+\frac{Z_1}{Z_2}} = \frac{1}{1+\frac{\frac{1}{R_{2g}}+j \omega C}{\frac{1}{R_1}+j \omega C_1}} = \frac{1}{1+\frac{R_1}{R_{2g}}\frac{1+j \omega R_{2g} C}{1+ j \omega R_1 C_1}} \end{equation}\]

Hieraus folgt dann die Bestimmungsgleichung für den Kondensator \(C_1\):

(70)\[\begin{equation} C_1 = \frac{R_{2g}}{R_1} C = \frac{0.5}{9} 10\,pF = 0.55\,pF. \end{equation}\]

RC-Spannungsteiler

Gegeben ist der abgebildete Spannungsteiler in Abb. 33 mit zwei Widerständen und einem Kondensator.

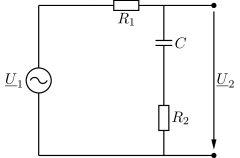
Abb. 33 RC-Spannungsteiler.

Spannungsverhältnis

Berechnen Sie den komplexen Spannungsübertragungsfaktor \(\underline{H}_u=\underline{U}_2/\underline{U}_1\).

Lösung

Fassen Sie die Bauteile zu Impedanzen \(Z_1\) und \(Z_2\) zusammen. Das gesuchte Spannungsverhältnis erhalten Sie aus der Spannungsteilerregel.

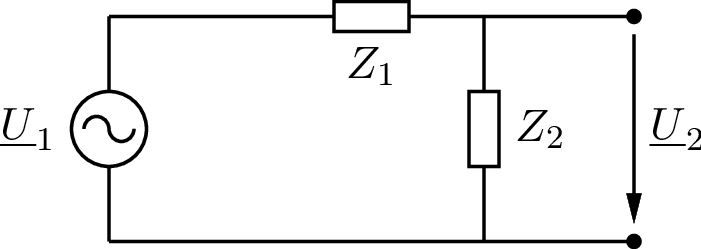
Abb. 34 RC-Spannungsteiler zusammengefasst.

(71)\[\begin{equation} \underline{Z}_1 = R_1 \underline{Z}_2 = R_2 + \frac{1}{j \omega C} \end{equation}\]

(72)\[\begin{equation} \underline{H} = \frac{\underline{U}_2}{\underline{U}_1} = \frac{\underline{Z}_2}{\underline{Z}_1+\underline{Z}_2} = \frac{R_2+\frac{1}{j \omega C}}{R_1+R_2+\frac{1}{j \omega C}} = \frac{1+j \omega R_2C}{1 + j \omega (R_1+R_2)C} \end{equation}\]

Betrag und Phase

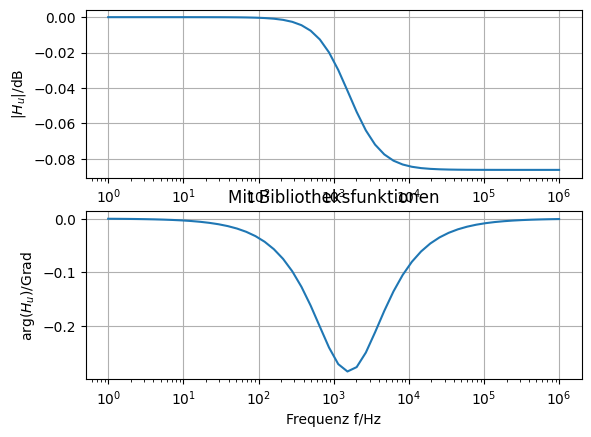
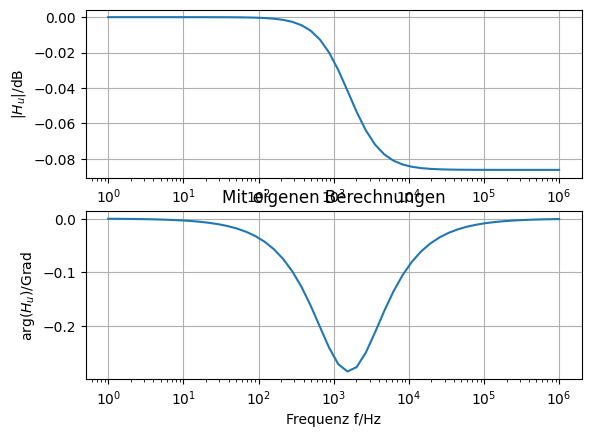
Stellen Sie den Betrag und den Phasenwinkel von \(\underline{H}_u\) als Funktion von \(\omega\) für den Fall \(R_1 = 1\,\Omega\), \(R_2 = 100\,\Omega\) und \(C = 1\,\mu F\) mit Python dar.

Lösung

Mit der Vorarbeit aus Spannungsteiler können Sie die Ausdrücke für Betrag und Phase der Spannungsübertragungsfunktion \(\underline{H}\) direkt ablesen. Der Betrag ist der Quotient der Beträge von Zähler und Nenner.

(73)\[\begin{equation} \vert \underline{H} \vert = \frac{\vert 1 + j \omega R_2 C \vert}{\vert 1 + j \omega (R_1+R_2) C \vert} = \frac{\sqrt{1 + (\omega R_2 C)^2}}{\sqrt{1+(\omega (R_1+R_2) C)^2}} = \sqrt{\frac{1 + (\omega R_2 C)^2}{1 + (\omega (R_1+R_2) C)^2}} \end{equation}\]

Für die Phase, das Argument von \(\underline{H}\), kann auch der Quotient der Argumente von Zähler und Nenner gebildet werden.

(74)\[\begin{equation} \arg(\underline{H}) = \frac{\arg(1 + j \omega R_2 C)}{\arg(1 + j \omega (R_1+R_2) C)} = \frac{\arctan(\omega R_2 C)}{\arctan(\omega (R_1+R_2) C)} = \arctan(\omega R_2 C) - \arctan(\omega (R_1+R_2) C) \end{equation}\]

import numpy as np
import matplotlib.pyplot as plt

# Definitionen

# Datenbereich
f = np.logspace(0, 6)  # Hz logarithmisch
w = 2 * np.pi * f

# Bauteilwerte
R1 = 1
R2 = 100
C = 1e-6

# Übertragungsfunktion
H_u = (1 + 1j * w * R2 * C) / (1 + 1j * w * (R1 + R2) * C)

# Erstellen des Bode-Diagramms

# Mit direkten Funktionen aus numpy
fig1 = plt.figure(1)
plt.subplot(2, 1, 1)
plt.semilogx(f, 20*np.log10(np.abs(H_u)))
plt.grid()
plt.ylabel(r'$\vert H_u \vert$/dB')
plt.subplot(2, 1, 2)
plt.semilogx(f, np.rad2deg(np.angle(H_u)))
plt.grid()
plt.ylabel(r'arg($H_u$)/Grad')
plt.xlabel(r'Frequenz f/Hz')
plt.title(r'Mit Bibliotheksfunktionen')


# Mit eigenen Berechnungen
# Betrag der Übertragungsfunktion
abs_H_u = 20*np.log10(np.sqrt((1 + np.square(w * R2 * C)) / (1 + np.square(w * (R1 + R2) * C))))

# Phase bzw. Argument der Übertragungsfunktion
arg_H_u = np.arctan(w * R2 * C) - np.arctan(w * (R1 + R2) * C)

fig2 = plt.figure(2)
plt.subplot(2, 1, 1)
plt.semilogx(f, abs_H_u)
plt.grid()
plt.ylabel(r'$\vert H_u \vert$/dB')
plt.subplot(2, 1, 2)
plt.semilogx(f, 180 / np.pi * arg_H_u)
plt.grid()
plt.ylabel(r'arg($H_u$)/Grad')
plt.xlabel(r'Frequenz f/Hz')
plt.title(r'Mit eigenen Berechnungen')

Text(0.5, 1.0, 'Mit eigenen Berechnungen')