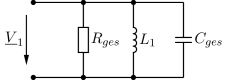
Leistungsanpassung und Schwingkreis

Leistungsberechnung

An eine Spannungsquelle mit der Leerlaufspannung \(\underline{U}_0\), der inneren Impedanz \(\underline{Z}_i=R_i+j\omega L_i\) und der Kreisfrequenz \(\omega\) ist ein Widerstand \(R_2\) angeschlossen. In Reihe mit dem Widerstand \(R_2\) soll ein Kondensator \(C_2\) geschaltet werden.

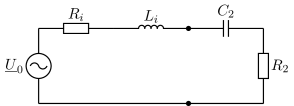
Abb. 43 Schaltung für die Leistungsberechnung.

Leistungsaufnahme

Leiten Sie einen Ausdruck für die Leistung in Abhängigkeit der gegebenen Größen her. Wählen Sie dabei eine Darstellungsform, so dass die Kapazität \(C_2=C_{opt}\) des Kondensators bestimmt werden kann, damit die vom Widerstand \(R_2\) aufgenommene mittlere Leistung möglichst groß wird.

Lösung

(81)\[\begin{align} \underline{S} &= \underline{U} \cdot \underline{I}^* \\ P &= \operatorname{Re}(\underline{S}) = \operatorname{Re}(\underline{U}_{R_2} \cdot \underline{I}^*) \\ &= \operatorname{Re}(R_2 \cdot \underline{I} \cdot \underline{I}^*) = R_2 \vert{\underline{I}}^2\vert \\ &= \frac{1}{2} R_2 \hat{I}^2 = R_2 I_{eff}^2 \\ \underline{I} &= \frac{\underline{U}_0}{R_i+R_2+j(\omega L_i-\frac{1}{\omega C_2})} \\ P &= R_2 \frac{\vert\underline{U}_0\vert^2}{\vert R_i+R_2+j(\omega L_i-\frac{1}{\omega C_2})\vert^2} \\ &= \frac{1}{2} R_2 \frac{\hat{U}_0^2}{(R_i+R_2)^2+(\omega L_i-\frac{1}{\omega C_2})^2} \\ &= \frac{R_2 U_{0,eff}^2}{(R_i+R_2)^2+(\omega L_i-\frac{1}{\omega C_2})^2} \end{align}\]

Daraus folgt, dass die Wirkleistung \(P\) im Resonanzfall maximal wird, wenn \((\omega L_i-\frac{1}{\omega C_2})=0\) gilt.

Bestimmung der Kapazität

Wie groß ist \(C_{opt}\) zu wählen für den Fall \(R_2=90\,\Omega\), \(R_i=10\,\Omega\), \(L_i=20\,mH\), \(U_0=141\,V\) und \(\omega=2\pi 100\,Hz\)

Lösung

\[\begin{split} \omega_0 = \frac{1}{\sqrt{L_i C_{opt}}} \\ C_{opt} = \frac{1}{\omega^2_0 L_i} = 127\,\mu F \end{split}\]

Maximale Leistung

Welche maximale Leistung nimmt der Widerstand \(R_2\) für den berechneten Fall auf?

Lösung

\[ P_{max} = \frac{1}{2} R_2 \frac{\hat{U}_0^2}{(R_i+R_2)^2} = 90\,W \]

Parallelresonanzkreis mit Übertrager

An einen Parallelresonanzkreis ist über einen idealen Übertrager mit dem Übersetzungsverhältnis ü=2 die Parallelschaltung eines Widerstandes \(R_2\) und eines Kondensators \(C_2\) angeschlossen. Die Werte der Bauteile lauten \(L_1=1\,\mu H\), \(C_1=100\,pF\), \(R_1=2\,k\Omega\), \(R_2=R_1\) und \(C_2=C_1\). Wie beeinflusst die Parallelschaltung aus \(R_2\) und \(C_2\) die Resonanzfrequenz und die Güte des Parallelschwingkreises?

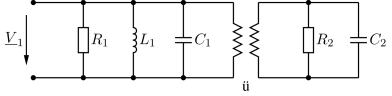
Abb. 44 Schaltung mit idealem Übertrager.

Ersatzschaltbild

Skizzieren Sie das Ersatzschaltbild der transformierten Parallelschaltung aus \(R_2\) und \(C_2\).

Lösung

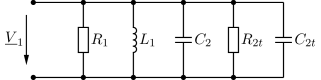
Abb. 45 Ersatzschaltbild mit transformierter Impedanz.

Impedanztransformation mit einem idealen Übertrager:

(82)\[\begin{align} Z_{2t} &= \mbox{ü}^2 Z_2 \\ Y_{2t} &= \frac{1}{R_{2t}} + j\omega C_{2t} = \frac{1}{\mbox{ü}^2}Y_2 \\ &= \frac{1}{\mbox{ü}^2}\left(\frac{1}{R_2} + j\omega C_2 \right) = \frac{1}{\mbox{ü}^2 R_2} + j \omega \frac{C_2}{\mbox{ü}^2} \\ R_{2t} &= \mbox{ü}^2 R_2 = 4 R_2 \\ C_{2t} &= \frac{C_2}{\mbox{ü}^2} = \frac{C_2}{4} \end{align}\]

Zusammenfassen

Fassen Sie gleichartige Zweipole zusammen.

Lösung

Abb. 46 Ersatzschaltbild mit zusammengefassten Zweipolen.

(83)\[\begin{align} \frac{1}{R_{ges}} &= \frac{1}{R_1} + \frac{1}{R_{2t}} = \frac{5}{4 R} \\ R_{ges} &= \frac{4}{5} R \\ C_{ges} &= C_1 + C_{2t} = \frac{5}{4} C \end{align}\]

Güte und Resonanz

Bestimmen Sie mit den Bezeichnungen aus der vorherigen Unteraufgabe die Resonanzfrequenz \(\omega_{0t}\) und die Güte \(Q_t\).

Lösung

(84)\[\begin{align} \omega_0 &= \frac{1}{\sqrt{L_1 C_1}} = 100\,MHz \\ \omega_{0t} &= \frac{1}{\sqrt{L_1 C_{ges}}} = \sqrt{\frac{4}{5}} \omega_0 = 89.44\,MHz \\ Q &= \frac{R_p}{\omega_0 L_p} = \frac{1}{G_p}\sqrt{\frac{C_p}{L_p}} = 20 \\ Q_t &= \frac{1}{G_{ges}}\sqrt{\frac{C_{ges}}{L_1}} = R_{ges}\sqrt{\frac{C_{ges}}{L_1}} \\ &= \frac{4}{5}\sqrt{\frac{5}{4}}Q = \sqrt{\frac{4}{5}} Q = 17.89 \end{align}\]