Anpassung und Wechselstrommessbrücke

Blindleistungskompensation

Ein Verbraucher \(\underline{Z}_L\) wird über eine näherungsweise verlustlose Leitung aus dem Netz versorgt (\(f\) = 50 Hz), \(U_{eff}\) = 230 V. Er nimmt eine Wirkleistung von \(P\) = 5 kW und eine Blindleistung von \(Q\) = 4,5 kvar auf.

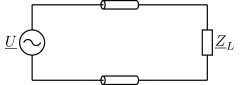
Abb. 39 Erstatzschaltbild des Versorgungsnetzes mit Verbraucher.

Leistungsfaktor

Wie groß ist der Leistungsfaktor \(\cos \phi\)?

Lösung

\[\begin{split} P = U_{eff} \cdot I_{eff} \cdot \cos \phi \\ Q = U_{eff} \cdot I_{eff} \cdot \sin \phi \\ \cos \phi = \frac{P}{S} = \frac{P}{\sqrt{P^2 + Q^2}} = 0,74 \end{split}\]

Auslegung

Für welchen Effektivwert des Stromes \(I_{eff}\) muß die Leitung ausgelegt sein?

Lösung

\[\begin{split} S = \sqrt{P^2 + Q^2} = U_{eff} \cdot I_{eff} = 6,73\,kVA \\ I_{eff} = 29,2\,A \end{split}\]

Zusätzlicher Verbraucher

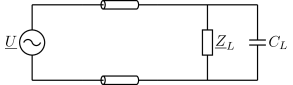
Abb. 40 Ersatzschaltbild des Versorgungsnetzes mit Verbraucher und zusätzlicher Kondensatorbatterie.

An die Anschlüsse des Verbrauchers wird zusätzlich eine Kondensatorbatterie von \(C_L\) = 188 \(\mu\)F parallel gelegt. Wie groß ist nun der Leistungsfaktor \(\cos \phi\) und der Effektivwert \(I_{eff}\) des Stromes?

Lösung

Der Gesamtstrom ist:

\[ \underline{I}_{ges} = \underline{I}_Z + \underline{I}_C = \frac{\underline{U}}{\underline{Z}} + j \omega C \underline{U} \]

Die Leistung an der Kondensatorbatterie:

(75)\[\begin{align} P_C &= \frac{1}{2} \underline{U}\underline{I}_{ges}^{*} \\ &= \frac{1}{2} \frac{\vert\underline{U}\vert^2}{\underline{Z}^{*}} - \frac{1}{2} j \omega C \vert\underline{U}\vert^2 \end{align}\]

Neue Wirk- und Blindleistung:

\[\begin{split} P_{neu} = P = 5\,kW \\ Q_{neu} = Q - \omega C U_{eff}^2 = 1,67\,kVA \end{split}\]

Daraus folgt der neue Leistungsfaktor:

\[ \cos \phi_{neu} = \frac{5\,kW}{\sqrt{(5\,kW)^2 + (1,64\,kVA)^2}} = 0.95 \]

Der Effektivwert des Stromes:

\[\begin{split} S_{neu} = \sqrt{P_{neu}^2 + Q_{neu}^2} = U_{eff} \cdot I_{eff,neu} = 5,26\,kVA \\ I_{eff,neu} = 23,2\,A \end{split}\]

Anpassung einer Heizeinrichtung

Zur Erwärmung von Werkstücken in einer Härteanlage wird ein Mittelfrequenzgenerator (\(f\) = 20 kHz bis 200 kHz) mit folgendem Ersatzschaltbild Abb. 41 eingesetzt.

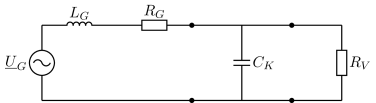
Abb. 41 Ersatzschaltbild des Mittelfrequenzgenerators.

Bei der Erhitzung durch Stromdurchgang wirkt das Werkstück als ohmscher Widerstand \(R_V\), dessen Wert durch die Abmessungen frei wählbar ist. Es wird an den Generator \(U_{G,eff}\) = 300 V, \(R_G\) = 18 \(\Omega\), \(L_G\) = 2 mH über ein Kabel angeschlossen, dessen Leitungskapazität \(C_K\) = 1,5 nF ist.

Bestimmen Sie den Wert von \(R_V\) und die Frequenz \(f_0\) für den Anpassungsfall, bei dem also die Leistungsaufnahme des Werkstückes maximal wird.

Lösung

\[\begin{split} Z_G = Z_V^* R_G + j \omega L_G = \left( \frac{R_V}{1+j \omega C_K R_V} \right)^* \\ R_G = \frac{R_V}{1 + (\omega C_K R_V)^2} L_G = \frac{R_V^2 C_K}{1 + (\omega C_K R_V)^2} \\ R_V = \frac{L_G}{C_K R_G} \omega^2=\frac{1}{L_G C_K} - \frac{R_G^2}{L_G^2} \\ R_V = 74,1\,k\Omega f = 91,9\,kHz \end{split}\]

Wie groß ist diese Leistung?

Lösung

(76)\[\begin{align} P_{total} &= \frac{U_{eff}^2}{R_G + \underbrace{\operatorname{Re}(Z_V)}_{=R_G}} = \frac{U_{eff}^2}{2 R_G} \\ P_V &= \frac{1}{2} P_{total} = \frac{U_{eff}^2}{4 R_G} = 1,25\,kW \end{align}\]

Alternativ auch Lösung über den Spannungsteiler

(77)\[\begin{align} U_{eff,V} &= \frac{\operatorname{Re}(Z_V)}{R_G + \operatorname{Re}(Z_V)} U_{eff} = \frac{1}{2} U_{eff} \\ P_V &= \frac{U_{eff,V}^2}{\operatorname{Re}(Z_V)} = \frac{1}{4} \frac{U_{eff}^2}{R_G} = 1,25\,kW \end{align}\]

Wien-Robinson-Brücke

Die abgebildete Wechselstrommessbrücke kann als Sperrfilter eingesetzt werden. Sie bildet auch den passiven Teil eines Wien-Robinson-Oszillators [].

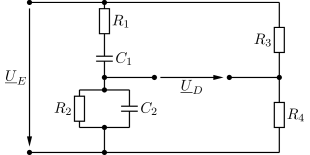
Abb. 42 Wien-Robinson-Brücke

Widerstandsverhältnis

Welches Widerstandsverhältnis \(R_3/R_4\) muss gewählt werden, wenn \(R_1=R_2=R\) und \(C_1=C_2=C\), damit die Brücke abgeglichen werden kann?

Lösung

Abgleichbedingung:

\[\begin{split} \frac{\underline{Z_1}}{\underline{Z_2}} = \frac{R_3}{R_4} \\ \left(R + \frac{1}{j \omega C}\right) \left(\frac{1}{R} + j \omega C\right) = \frac{R_3}{R_4} \\ 2 + j \omega RC + \frac{1}{j \omega RC} = \frac{R_3}{R_4} \\ \end{split}\]

Wenn man Real- und Imaginärteil der rechten und linken Seite vergleicht (Abgleich), so kann die Brücke nur abgeglichen werden, wenn das Widerstandsverhältnis \(R_3/R_4 = 2\) ist.

Kreisfrequenz

Für welche Kreisfrequenz \(\omega_A\) ist die Brücke bei \(R_3=2 R_4\) abgeglichen?

Lösung

Die Brücke ist abgeglichen, somit folgt

\[\begin{split} j \omega_A RC + \frac{1}{j \omega_A RC} = 0 \\ \omega_A RC = \frac{1}{\omega_A RC} \\ \omega_A = \frac{1}{RC} \\ \end{split}\]

Ortskurve

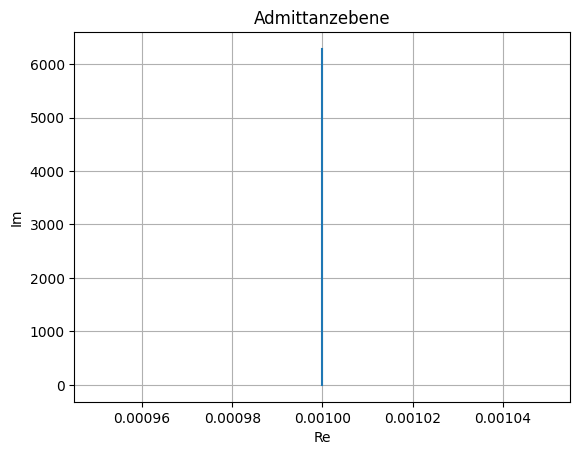
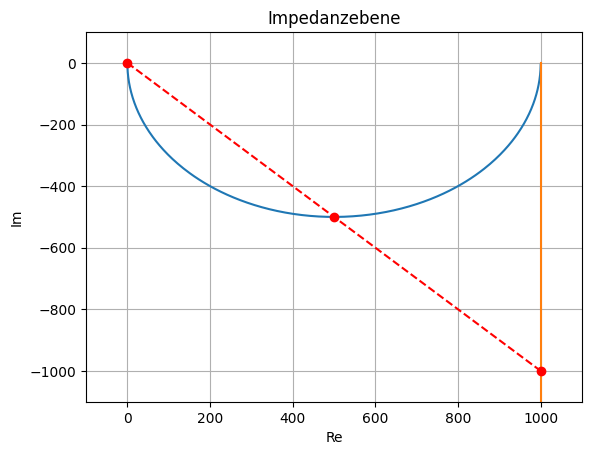
Zeichnen Sie die Ortskurve von \(Z_1(\omega) = R_1 + 1/(j \omega C_1)\) und \(Z_2=R_2 || C_2\) in einem Diagramm. Markieren Sie die Punkte \(Z_1(\omega_A)\) und \(Z_2(\omega_A)\) in den Ortskurven der beiden Impedanzen.

Lösung

Bei \(\omega = \omega_A\) ist \(\underline{Z}_1 / \underline{Z}_2 = 2 / 1\) und gleichen Verhältnissen auf den Achsen (Re und Im) ist der Graph durch \(\underline{Z}_1(\omega_A)\) und \(\underline{Z}_2(\omega_A)\) eine Gerade, deren Mittelpunkt auf der Ortskurve von \(\underline{Z}_2\) liegt.

# %% Bibliotheken
import numpy as np
import matplotlib.pylab as plt

# %% Def. der Variablen
R = 1e3
C = 1e-6
wA = 1/(R*C)

f = np.logspace(0, 9, 1000)
w = 2 * np.pi * f


# %% Def. der Impedanzen/Admittanzen
Y2 = 1 / R + 1j * w * C
Z2 = 1. / Y2
Z1 = R + 1 / (1j * w * C)

x1 = [0, 500, 1000]
y1 = [0, -500, -1000]

# %% Ortskurven
fig1 = plt.figure(1)
plt.title('Admittanzebene')
plt.plot(Y2.real, Y2.imag)
plt.xlabel('Re')
plt.ylabel('Im')
plt.grid()
plt.show()

fig2 = plt.figure(2)
plt.title('Impedanzebene')
plt.plot(Z2.real, Z2.imag, Z1.real, Z1.imag)
plt.plot(x1, y1, '--', marker='o', color='red')
plt.xlabel('Re')
plt.ylabel('Im')
plt.grid()
plt.axis([-100, 1100, -1100, 100])
plt.show()

Übertragungsfaktor

Berechnen Sie das Spannungsübertragungsverhältnis \(\underline{H}_v = \underline{U}_D / \underline{U}_E\) von Ausgangs- zu Eingangsspannung. Stellen Sie den Betrag und den Phasenwinkel von \(\underline{H}_v\) als Funktion von \(\omega/\omega_A\) dar!

Lösung

Maschenumlauf: \(\underline{U}_2 - \underline{U}_4 - \underline{U}_D = 0\)

(78)\[\begin{align} \underline{U}_2 &= \frac{\underline{Z}_2}{\underline{Z}_1+\underline{Z}_2} \underline{U}_E \\ \underline{U}_4 &= \frac{R_4}{R_3+R_4} \underline{U}_E \\ \underline{U}_D &= \underline{U}_4 - \underline{U}_2 \\ &= \left( \frac{R_4}{R_3+R_4} - \frac{\underline{Z}_2}{\underline{Z}_1+\underline{Z}_2} \right) \underline{U}_E \\ &= \left( \frac{1}{1+\frac{R_3}{R_4}} - \frac{1}{1 + \frac{\underline{Z}_1}{\underline{Z}_2}} \right) \underline{U}_E \end{align}\]

Hieraus folgt das Spannungsübertragungsverhältnis:

(79)\[\begin{align} \underline{H}_u &= \frac{\underline{U}_D}{\underline{U}_E} \\ &= \frac{1}{1 + 2} - \frac{1}{1 + (2 + j \omega RC + \frac{1}{j \omega RC})} \\ &= \frac{1}{3} \left( 1 - \frac{1}{1 + j \frac{1}{3}(\omega RC - \frac{1}{\omega RC})}\right) \\ &= \frac{1}{3} \frac{j \frac{1}{3}(\omega RC - \frac{1}{\omega RC})}{1 + j \frac{1}{3}(\omega RC - \frac{1}{\omega RC})} \\ &= \frac{1}{3} \frac{1}{1 - j \frac{3}{\omega RC - \frac{1}{\omega RC}}} \\ &= \frac{1}{3} \frac{1}{1 - j \frac{3}{\omega / \omega_A - \omega_A / \omega}} \end{align}\]

Betrag und Phase des Spannungsübertragungsverhältnisses:

(80)\[\begin{align} \vert\underline{H}_u\vert &= \frac{1}{3 \sqrt{1 + \left(\frac{3}{\omega/\omega_A - \omega_A/\omega}\right)^2}} \\ \arg(\underline{H}_u) &= \arctan(\frac{3}{\omega/\omega_A - \omega_A/\omega}) \end{align}\]

Literaturverzeichnis