Bode-Diagramm und Nyquist-Ortskurve

Schaltungsanalyse mit dem Bode-Diagramm

Im Labor ist mit einem Vektornetzwerkanalysator das Bode-Diagramm eines Zweitors aufgenommen worden. In Abb. 35 sind Betrag \(\vert H_u \vert\) und Phase \(\arg(H_u)\) der Spannungsübertragungsfunktion von Tor 1 auf Tor 2, \(\underline{H}_u=\underline{U}_2/\underline{U}_1\), abgebildet.

Abb. 35 Bode-Diagramm des Zweitors

Funktion

Welche Funktion erfüllt das gemessene Zweitor?

Lösung

Das gemessene Zweitor hat die Funktion eines Hochpassfilters.

Bauteilanordnung

Welche Bauteilanordnung vermuten Sie zwischen den zwei Toren? Zeichnen Sie ein Ersatzschaltbild des Zweitors mit Eingangsspannung \(\underline{U}_1\) und Ausgangsspannung \(\underline{U}_2\).

Lösung

In einfachster Ausführung kann man einen Hochpass durch einen Spannungsteiler mit Kapazität \(C\) und Widerstand \(R\) realisieren.

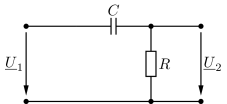
Abb. 36 Einfacher RC-Hochpass, Zweitor-Ersatzschaltbild

Spannungsübertragungsfunktion

Leiten Sie die Spannungsübertragungsfunktion, \(\underline{H}_u=\underline{U}_2/\underline{U}_1\), Ihres Ersatzschaltbildes her.

Lösung

\[ \underline{H}_u=\frac{\underline{U}_2}{\underline{U}_1} = \frac{j \omega R C}{1+j \omega R C} \]

Betrag und Phase

Bestimmen Sie Betrag und Phase der Spannungsübertragungsfunktion \(\underline{H}_u\).

Lösung

\[ \vert\underline{H}_u\vert =\frac{\omega R C}{\sqrt{1 + (\omega R C)^2}} \]

\[ \varphi(\underline{H}_u) = \arg(\underline{H}_u) = \arg \left(\frac{j \omega R C}{1+j\omega R C}\right) = \arg \left( \underbrace{\frac{(\omega R C)^2}{1+(\omega R C)^2}}_{\operatorname{Re}} + j \underbrace{\frac{\omega R C}{1 + (\omega R C)^2}}_{\operatorname{Im}} \right) = \arctan\left(\frac{1}{\omega R C}\right) \]

3 dB-Grenzfrequenz

Leiten Sie eine Bestimmungsgleichung für die 3 dB-Grenzfrequenz \(f_g\) der Spannungsübertragungsfunktion her.

Bemerkung

Die Grenzfrequenz kennzeichnet die Frequenz, bei der der Betrag auf -3 dB abfällt und die Phase 45 Grad beträgt.

Lösung

Es gibt zwei Lösungswege:

\[ \vert H_u \vert = -3\,dB = \frac{1}{\sqrt{2}}_{lin} = \frac{\omega_g R C}{\sqrt{1+(\omega_g R C)^2}} \arg(H_u) = \frac{\pi}{4} = \arctan\left(\frac{1}{\omega_g R C}\right) \]

\[ \Rightarrow f_g = \frac{1}{2 \pi R C} \Rightarrow f_g = \frac{1}{2 \pi R C} \]

Alternativ auch der Ansatz aus der Elektronik-Fibel:

\[ R = X_C \]

\[ R = \frac{1}{\omega_g C} \]

\[ R = \frac{1}{2 \pi f_g C} \]

\[ \Rightarrow f_g = \frac{1}{2 \pi R C} \]

Grenzfrequenz

Wie groß ist die Grenzfrequenz für \(R=1\,k\Omega\) und \(C=100\,nF\)?

Lösung

\[ \omega_g = \frac{1}{R C} = 10\,kHz \]

\[ f_g = \frac{1}{2 \pi R C} \approx 1.6\,kHz \]

Ortskurve einer Zweipol-Admittanz

Konstruieren Sie eine Ortskurve der Admittanz \(Y(\omega)\) für den skizzierten Zweipol in Abb. 37. Überprüfen Sie das Ergebnis, indem Sie ausgezeichnete Frequenzwerte betrachten. Die Werte der Bauteile lauten \(R_s = 50\,\Omega\), \(R_p = 200\,\Omega\) und \(C = 2\,\mu F\).

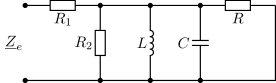
Abb. 37 Zweipol-Admittanz

Ortskurve mit verschiedenen Parametern

Gegeben sei nachfolgende RLC-Schaltung in Abb. 38. Die Werte der Bauteile lauten \(R_1 = 60\,\Omega\), \(R_2 = 200\,\Omega\), \(L = 200\,\mu H\) und \(C = 5\,nF\).

Abb. 38 RLC-Schaltung

Ortskurve mit \(\omega\) als Parameter

\(f(\omega)\) Konstruieren Sie die Ortskurve der Eingangsimpedanz \(\underline{Z}_e\) mit der Kreisfrequenz \(\omega\) als Parameter, \(0 \leq \omega \leq \infty\). Dabei sei der Widerstand \(R = 200\,\Omega\).

Lösung

\[ \underline{Y}_p = \frac{1}{\underline{Z}_p} = \underbrace{\frac{1}{R} + \frac{1}{R_2}}_{\frac{1}{R_3}=10\,mS} + \frac{1}{j\omega L} + j\omega C \]

• Ortskurve für \(\underline{Y}_p(\omega)=\frac{1}{R_3}+j(\omega C - \frac{1}{\omega L} )\) zeichnen, eine Gerade.

• Ortskurve invertieren, \(\underline{Y}_p \rightarrow \underline{Z}_p\), ergibt einen Kreis. \(\underline{Z}_p(\omega_0)=R_3=100\,\Omega\), Resonanzkreisfrequenz \(\omega_0=\frac{1}{\sqrt{LC}}\), \(\underline{Z}_p(\infty)=\underline{Z}_p(0)=0\)

• Ortskurve verschieben, \(\underline{Z}_e(\omega)=\underline{Z}_p(\omega) + R_1\)

# %% Import der Bibliotheken
import numpy as np
import matplotlib.pylab as plt

# %% Definition der Variablen
R = 200.0
R1 = 60.0
R2 = 200.0
L = 200e-6
C = 5e-9

f = np.logspace(0, 9, 1000)
w = 2 * np.pi * f

# %% Definition der Impedanzen/Admittanzen
Yp = 1 / R + 1 / R2 + 1 / (1j * w * L) + 1j * w * C
Zp = 1 / Yp
Ze = Zp + R1

# %% Ortskurven plotten
fig1 = plt.figure(1)
plt.title('Admittanzebene')
plt.plot(np.real(Yp), np.imag(Yp))
plt.xlabel('Re')
plt.ylabel('Im')
plt.legend(('Yp'))
plt.grid()
plt.show()

fig2 = plt.figure(2)
plt.title('Impedanzebene')
plt.plot(np.real(Zp), np.imag(Zp), np.real(Ze), np.imag(Ze))
plt.xlabel('Re')
plt.ylabel('Im')
plt.axis([0, 200, -55, 55])
plt.legend(('Zp', 'Ze'))
plt.grid()
plt.show()

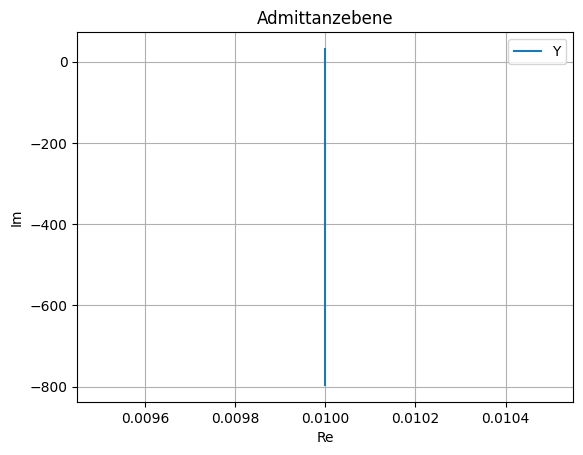
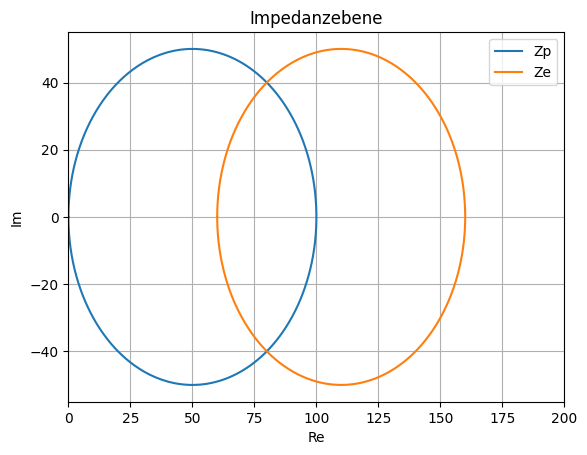
Ortskurve mit R als Parameter

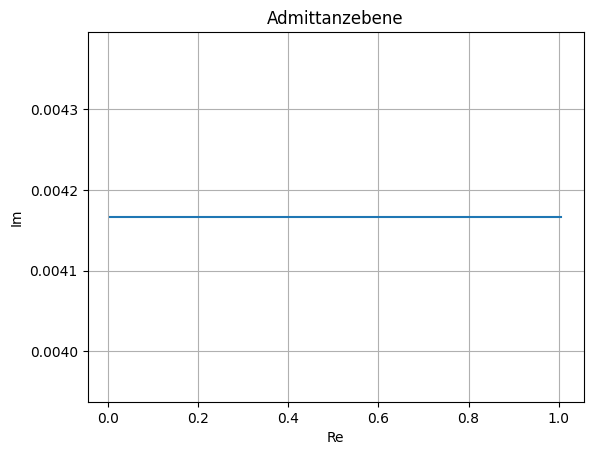
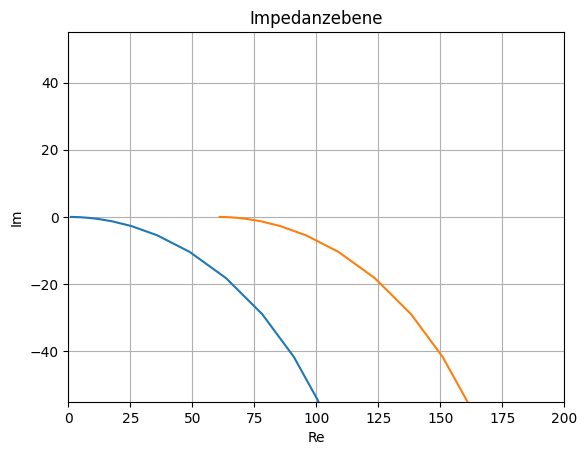
Konstruieren Sie die Ortskurve der Eingangsimpedanz \(\underline{Z}_e\) mit dem Widerstand R als Parameter, \(0 \leq R \leq \infty\). Dabei sei die Kreisfrequenz \(\omega = 1.5e6 1/s\).

Lösung

\[ \underline{Y}_p = \frac{1}{R_3} + j 4.17\,mS \]

\(R_3\) ist Funktion von \(R\), \(R_3=R_3(R)\), mit \(R=0 \Rightarrow R_3 = 0\) und \(R \rightarrow \infty \Rightarrow R_3 \rightarrow R_2 = 200\,\Omega\)

• \(\underline{Y}_p(R_3)\) zeichnen: Teil einer horizontalen Geraden in der komplexen Ebene \(0 \leq R_3 \leq 200\,\Omega\) bzw. \(5\,mS \leq \frac{1}{R_3} \leq \infty\)

• Ortskurve invertieren, dazu

  • die gesamte Gerade invertieren \(\rightarrow\) Kreis

  • Anfangspunkt von \(\underline{Y}_p\) invertieren

  \(\Rightarrow \underline{Z}_p\) ist ein Kreisabschnitt.

• Ortskurve verschieben, \(\underline{Z}_e=\underline{Z}_p + R_1\).

# %% Bibliotheken
import numpy as np
import matplotlib.pylab as plt

# %% Def. der Variablen
R1 = 60
R2 = 200
L = 200e-6
C = 5e-9

w = 1.5e6
R = np.logspace(0, 9)

# %% Def. der Impedanzen/Admittanzen
Yp = 1 / R + 1 / R2 + 1 / (1j * w * L) + 1j * w * C
Zp = 1. / Yp
Ze = Zp + R1

# %% Ortskurven
fig1 = plt.figure(1)
plt.title('Admittanzebene')
plt.plot(Yp.real, Yp.imag)
plt.xlabel('Re')
plt.ylabel('Im')
plt.grid()
plt.show()

fig2 = plt.figure(2)
plt.title('Impedanzebene')
plt.plot(Zp.real, Zp.imag, Ze.real, Ze.imag)
plt.xlabel('Re')
plt.ylabel('Im')
plt.grid()
plt.axis([0, 200, -55, 55])
plt.show()